Démonstration
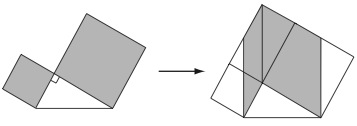
Nous avons pu conjecturer (voir introduction), que dans un triangle rectangle en nous avons :
Cela signifie que si nous construisons un carré de coté et un carré de coté nous aurons la somme de leurs aire égale à l'aire d'un carré de coté .
De nombreuses démonstrations du théorème de Pythagore on été proposées.
La démonstration présentée ici est purement géométrique.
Construisons donc les carrés et extérieurs au triangle , ainsi que le carré qui inclut le triangle .
On nomme le point d'intersection des droites et .
Par hypothèse, nous avons et , donc .
Or et , les triangles et sont donc semblables et est rectangle en .
Les points , , et sont donc alignés et . En effet, est un rectangle et .
Nous pouvons prouver de la même manière que les points , , et sont alignés et que .
Le triangle est donc rectangle en et semblable au triangle .
L'aire d'un parallélogramme ne dépend que de la longueur d'un de ses cotés et de la hauteur associée (voir Aires des figures usuelles).
Ainsi, si nous construisons un parallélogramme avec , nous aurons :
De même, si nous construisons un parallélogramme avec , nous aurons :
Observons ce qui se passe si les points et sont confondus et que les points et sont confondus :
Les points , et sont confondus et forment un hexagone dont nous connaissons l'aire :
Nous avons donc :
D'autre part nous avons :
Or, les triangles et sont semblables,
Nous avons donc
Soit
Or
Nous avons donc, finalement :
Le théorème de Pythagore est ainsi démontré.