2. Eigenschaften ganzrationaler Funktionen
Wir summieren Potenzfunktionen und erhalten die Polynomfunktion.
Übertrage den Hefteintrag und sieh dir das Erklärvideo dazu an.
HE_ganzrationale Funktionen
Erklärvideo
Genauer befassen wir uns noch in einem späteren Kapitel mit dem Verhalten von Funktionen im Unendlichen. Jetzt sollst du aber trotzdem den ungefähren Verlauf einer ganzrationalen Funktion erkennen können. Ein kleiner Ausblick auf das Unendliche bietet das untere Beispiel.
Schau dir im Applet darunter auch ein paar ganzrationale Funktionen an, damit du ein Gefühl für sie bekommst.

Im folgenden Applet kannst du dir Polynomfunktionen (max. bis Grad 4) ansehen. Eine ganzrationale Funktion dritten Grades erhältst du, wenn du einfach gleich Null setzt.

Lösung
Rechne hier Teilaufgabe a) bis f). Du musst nicht den gesamten Term ausmultiplizieren. Nur die höchste Potenz ist für uns hier wichtig.
Buch S. 113

Lösung
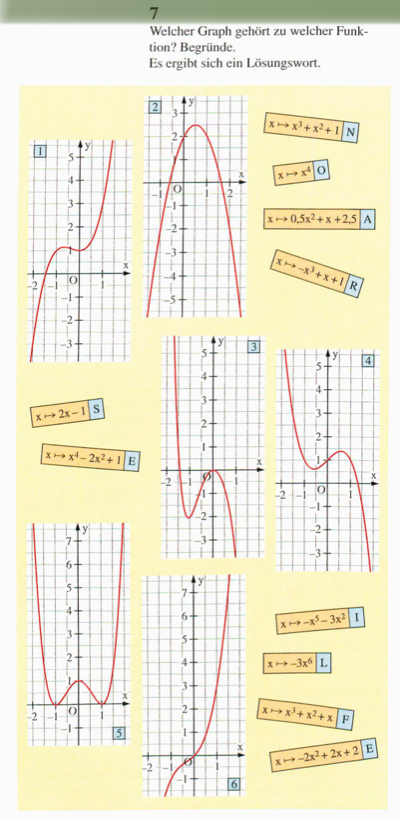
Lösungswort
Konzentriere dich in der nächsten Aufgabe auf die Teilaufgaben b), c) und d). Für c) und d) brauchst du deinen CAS-Rechner.
Tipp: Du hast vier Variablen und vier Punkte gegeben und kannst damit 4 Gleichungen aufstellen. Das musst du in deinen CAS füttern.

Lösung
freiwillige Übung
