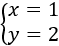Sistemas de ecuaciones: método gráfico
Como es de esperar, el método gráfico consiste en representar las gráficas asociadas a las ecuaciones del sistema para deducir su solución. La solución del sistema es el punto de intersección entre las gráficas. La razón de ello es que las coordenadas de dicho punto cumplen ambas ecuaciones y, por tanto, es la solución del sistema.
Como vamos a trabajar con sistemas de dos ecuaciones lineales con dos incógnitas (x e y), la gráfica de cada ecuación es una recta. Como consecuencia, la intersección de las gráficas es un único punto (a, b)
y la solución del sistema es x = a e y = b. No obstante, si las rectas son paralelas (no se cortan), el sistema no tiene solución, y si son iguales hay infinitas soluciones.
Para poder aplicar el método gráfico debemos saber representar las gráficas de las rectas. Nosotros lo haremos uniendo puntos calculados previamente.
Ejemplo
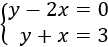
Resolución:
Lo primero que hacemos es despejar la y en ambas ecuaciones.
Primera ecuación:
Resolución:
Lo primero que hacemos es despejar la y en ambas ecuaciones.
Primera ecuación:
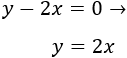
Segunda ecuación:
Segunda ecuación:
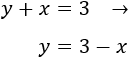
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizamos, por ejemplo, x = 0 y x = 2.
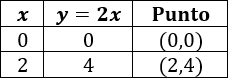
Para la primera función tenemos la tabla
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizamos, por ejemplo, x = 0 y x = 2.
Para la primera función tenemos la tabla
Para la segunda función tenemos la tabla (utilizando los mismos valores para x):
Para la segunda función tenemos la tabla (utilizando los mismos valores para x):
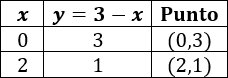
Representamos los puntos de las tablas y los unimos:
Representamos los puntos de las tablas y los unimos:
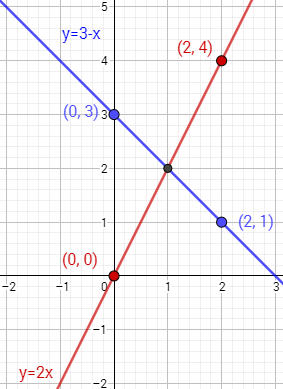 La solución del sistema es el punto donde las gráficas se cortan:
La solución del sistema es el punto donde las gráficas se cortan: