Voorbeeld + opgave 21 en 22
Voorbeeld
Gegeven is de functie f met f(x) =4−x2 .
Bereken het differentiaalquotiënt voor x = 1 en beschrijf de betekenis van dit getal.
Oplossing:
Maak een rij met differentiequotiënten door bij het interval [1,1+h] voor h steeds kleinere waarden te kiezen. Bijvoorbeeld:
Deze rij getallen lijkt te naderen naar -2 .
Dit is het differentiaalquotiënt van deze functie voor x = 1 en de veranderingssnelheid van de grafiek voor die waarde van x .
Het is ook het hellingsgetal van de raaklijn aan de grafiek voor x = 1.
Met dy/dx op de grafische rekenmachine kun je controleren dat dat inderdaad zo is.
Met dit hellingsgetal en beide coördinaten van het raakpunt kun je de vergelijking van de raaklijn opstellen.
Het hellingsgetal van de raaklijn is -2 . Er geldt daarom y = -2x+b
De raaklijn gaat door het raakpunt (1,3) . Hieruit volgt: -2⋅1+b=3 en dus b = 5
De vergelijking van de raaklijn wordt daarmee y = -2x+5
| interval | differentiequotiënt |
| [1;1,1] | -2,1 |
| [1;1,01] | -2,01 |
| [1;1,001] | -2,001 |
| [1;1,0001] | -2,0001 |
Opgave 21
Gegeven is de grafiek van f(x) = 0,5x3+2.
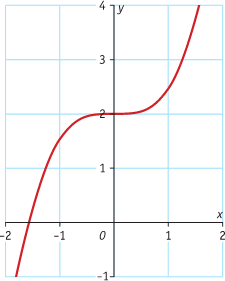
a. Maak een rij met differentiequotiënten op het interval [1,1+h] waarin h achtereenvolgens de waarden 0,1 ; 0,01 ; 0,001 en 0,0001 heeft.
b. Hoe groot is het differentiaalquotiënt voor x = 1?
c. Teken de grafiek van f en teken bij x = 1 de raaklijn aan de grafiek. Controleer of de richtingscoëfficiënt van die raaklijn ongeveer overeenkomt met de bij b gevonden waarde. Stel een vergelijking van die raaklijn op.
Opgave 22
Gegeven is de functie f(x) = -x2−4x+8.
a. Bereken
door hele kleine intervallen te nemen. Controleer je antwoord met de grafische rekenmachine.
b. Stel de formule op van de raaklijn aan de grafiek van f voor x = 2.