Relação entre volume e área
Área da Superfície Esférica a Partir de seu Volume
Para esta demonstração iremos utilizar apenas conceitos básicos de Geometria Podemos decompor a esfera em uma infinidade de pirâmides cujas bases compõem a superfície esférica e os vértices se encontram no centro da esfera.
Desta forma, a superfície da esfera fica dividida em N polígonos e a área da superfície esférica ASE é dada por:
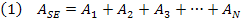Para o Volume da esfera, podemos dizer que é igual à soma dos volumes dessasN por:
Sabemos que o volume de uma pirâmide é dado pela fórmula:
No caso destas pirâmides que compõem a esfera, suas alturas são exatamente o raio R da esfera. Assim, a relação (3) fica:
e o volume da esfera será a soma dos volumes destas pirâmides:
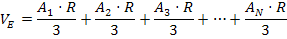
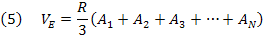Vejam que a soma das áreas da relação (5) é igual à superfície esférica dada na relação (1). Assim, temos que:
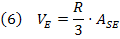Partindo do princípio em que já sabemos como calcular o volume da esfera:
podemos determinar a superfície esférica substituindo a relação (7) em (6), obtendo:
Vejam que aqui só utilizamos conceitos básicos de Geometria, levando em conta que já sabíamos previamente a fórmula do volume da esfera.
Desta forma, a superfície da esfera fica dividida em N polígonos e a área da superfície esférica ASE é dada por:
Para o Volume da esfera, podemos dizer que é igual à soma dos volumes dessasN por:
Sabemos que o volume de uma pirâmide é dado pela fórmula:
No caso destas pirâmides que compõem a esfera, suas alturas são exatamente o raio R da esfera. Assim, a relação (3) fica:
e o volume da esfera será a soma dos volumes destas pirâmides:
Vejam que a soma das áreas da relação (5) é igual à superfície esférica dada na relação (1). Assim, temos que:
Partindo do princípio em que já sabemos como calcular o volume da esfera:
podemos determinar a superfície esférica substituindo a relação (7) em (6), obtendo:
Vejam que aqui só utilizamos conceitos básicos de Geometria, levando em conta que já sabíamos previamente a fórmula do volume da esfera.