Test jezelf
Vraag 1
Je ziet een aantal punten op een grafiek.
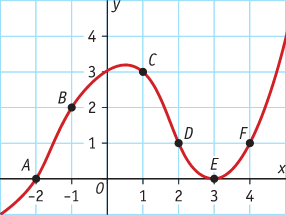
a. Bereken de helling van het lijnstuk AB.
b. Bereken de helling van de lijn door C en F.
c. Bij welke getekende punten hoort een differentiequotiënt van 0 ? (Er zijn twee mogelijkheden)
d. Punt F heeft een kleinere y -waarde dan punt C. Hoe kun je dat aan het differentiequotiënt op het interval [1,4] zien?
Vraag 2
Gegeven is de functie f(x) = x2 + 7x + 12.
a. Bereken de gemiddelde verandering van f op het interval [2,6].
b. Bereken het differentiequotiënt van f op het interval [-4,9].
c. Geef een interval waarop de gemiddelde verandering van f gelijk is aan 0.
Vraag 3
Bij een wielrenner in een vlakke tijdrit worden op bepaalde plaatsen tussentijden genoteerd. Die vind je in de tabel.
a. Bereken het differentiequotiënt op het tijdsinterval [0,10] en geef de betekenis hiervan.
b. Je maakt bij deze tabel een grafiek door de punten met lijnstukken te verbinden. Op de horizontale as komt de tijd t in minuten, op de verticale as de afgelegde afstand a in km. Bereken het hellingsgetal van het lijnstuk dat hoort bij het interval [44,60] en geef de betekenis hiervan.
c. Bereken voor het tijdsinterval [18,44] de waarde in twee decimalen nauwkeurig.
d. Heeft de wielrenner zijn krachten goed verdeeld? Licht je antwoord toe.
| tijd t (min) | 0 | 10 | 18 | 34 | 44 | 60 | 78 | 94 |
| afstand a (km) | 0 | 8 | 12 | 18 | 23 | 29 | 37 | 45 |
Vraag 4
Gegeven is de functie f(x) = 3x2. Toon aan dat het differentiequotiënt van f op elk interval [a,a+1] gelijk is aan 6⋅a+3.
Vraag 5
Teken bij deze tabel met differentiequotiënten een passende grafiek.
| interval | differentiequotiënt |
| [0,1] | -2 |
| [1,2] | -1 |
| [2,3] | 0 |
| [3,4] | 1 |
| [4,5] | 2 |