Trost und Moral in der Mathematik
In "Humor in der Mathematik" (5. Auflage, Seite 18) habe ich folgende Aufgabe von Franz Rellich gefunden, die ich der Anschauung halber zuerst mit Geogebra und danach analytisch löse:
Ein Student geht auf der Weender Straße in Göttingen hinter einem Mädchen mit auffallend schönen Beinen her.
Frage: In welcher Entfernung muss der Student hinter dem Mädchen hergehen, um die Beine, so weit sie unter dem Rock hervorschauen, unter dem größtmöglichen Blickwinkel zu sehen?
Die Höhe des Rocksaumes über dem Erdboden sei dabei 60cm und die Augenhöhe des Studenten 178cm.
Rellich pflegte hinzuzufügen: Der Trost dabei ist, dass die gesuchte Entfernung nicht unendlich ist, und die Moral, dass sie nicht Null ist.
Da sowohl die Durchschnittsgröße der Studenten als auch die Rocksaumhöhen von Mädchen mit hübschen Beinen seit der Entstehungszeit dieser Aufgabe gewachsen sind, lassen sich in der unten stehenden Geogebra-Anwendung beide Parameter mit Hilfe von Schiebereglern variieren.
Außerdem kann man auf diese Weise den Einfluss dieser beiden Größen studieren.
Die Darstellung geht davon aus, dass sich der Student bei x=0 befindet und das Mädchen bei der pinkfarbenen senkrechten Linie.
Der Abstand der beiden lässt sich mit dem Schieberegler "Entfernung" einstellen oder durch Klick auf die kleine Schaltflläche unten links als Animation automatisch variieren.
Bei Veränderung des Abstands hinterlässt der rote Punkt eine Spur, die über alle eingenommenen Abstandswerte (x-Achse) den Blickwinkel im Bogenmaß nach oben abträgt, so dass man das Maximum leicht identifizieren kann.
Um alle Spitzfindigkeiten im Keim zu ersticken, muss wohl noch erwähnt werden, dass der horizontale Abstand des Rocksaums von den Beinen vernachlässigt wird, was auch zu der extrem magersüchtigen Darstellung des Mädchens als Linie passt.
In grau ist der Blickwinkel im Bogenmaß als Funktion des Abstandes mit den Parametern Augen- und Rocksaumhöhe eingezeichnet. Das Maximum ist mit einem schwarzen Punkt markiert, der bei Veränderung der Parameter ebenfalls eine Spur hinterlässt.
Durch Klick auf das Icon in der oberen rechten Ecke wird alles auf die Anfangsdarstellung zurückgesetzt.
Die Aufgabe stammt aus einer Zeit, als es noch völlig unverfänglich war und sogar als humorvoll galt, die Wirkung weiblicher Reize auf Mathematikstudenten zum Gegenstand von Rechenübungen zu machen.
Heute befürchte ich bitterböse Kommentare und versichere deswegen vorsorglich, dass es mir keineswegs darum geht, Frauen als Sexobjekt zu erniedrigen oder sonst in irgendeiner Weise zu diskriminieren.
Ich zitiere diese Aufgabe ausschließlich aus mathematikhistorischem Interesse und weil mich ihre Lösung interessiert. Außerdem finde ich, dass sie die männliche Interessenlage recht wirklichkeitsnah widerspiegelt, und für die Akzeptanz mathematischer Übungen ist ein Realitätsbezug nun einmal sehr wichtig.
Trotz der mit einem einfachen Satz zu definierenden Problemstellung beinhaltet der Lösungsweg gute Übungen zur Trigonometrie und zur Kurvendiskussion.
Kommen wir nun zur analytischen Lösung des Problems:
Rechnungen mit Winkeln sind immer dann besonders einfach, wenn diese zu rechtwinkligen Dreiecken gehören.
Unmittelbar trifft diese Aussage für den Blickwinkel nicht zu, aber er lässt sich als Differenz zweier Winkel ausdrücken, zu denen man die folgenden rechtwinkligen Dreiecke finden kann:
Im einen Fall des grünen Dreiecks ist die Hypothenuse die Verbindungslinie Augen - Rocksaum, im Fall des blauen Dreiecks die Verbindungslinie Augen - Füße des Mädchens.
Eine Kathete ist in beiden Fällen die Entfernung.
Die zweite ist beim blauen Dreieck die Augenhöhe, beim grünen ist es die Differenz aus Augen- und Rocksaumhöhe.
In beiden Dreiecken sind beide Katheten bekannt, so dass sich die Winkel mit Hilfe der Arkustangens-Funktion berechnen lassen.
Der Blickwinkel ergibt sich dann zu:
Blickwinkel = arctan ( Entfernung / ( Augenhöhe − Rocksaumhöhe ) ) − arctan ( Entfernung / Augenhöhe )
Variieren Sie die Parameter, um ihren Einfluss auf die Lage des Maximums zu erkennen!
Zu dieser Funktion muss man nun das Maximum finden, indem man die Ableitung berechnet und deren Nullstellen findet. Daserledigt entweder Geogebra oder man berechnet die Nullstellen der Ableitung wie folgt:
Die Ableitung der Arkustangensfunktion ist:
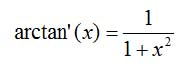
In unserem Beispiel ist die Entfernung die unabhängige Variable x und der Blickwinkel wird als Funktionswert y berechnet, so dass obige Formel mit x und y geschrieben etwas vertrauter so aussieht:
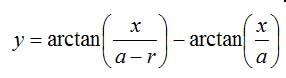
Beim Ableiten dieser Funktion kommt die Summenregel (alle Summanden werden separat abgeleitet) und die Kettenregel(Multiplikation der äußeren mit der inneren Ableitung) zum Einsatz und man erhält:
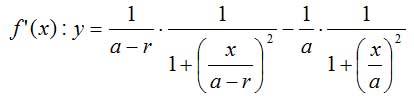
Zur Vereinfachung umgeformt:
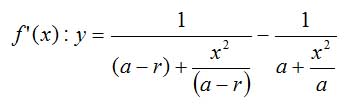
Die Funktionswerte dieser Ableitung sind die Steigung der Tangente an die Blickwinkelfunktion an der Stelle x. Das Maximum des Blickwinkels, das wir ja suchen, zeichnet sich dadurch aus, dass die Tangente dort horizontal verläuft, ihre Steigung dort also Null ist. Um es zu finden, setzen wir deshalb die Ableitungsfunktion gleich Null, lösen nach x auf und erhalten alle Stellen, an denen sich ein Maximum des Blickwinkels befinden kann:
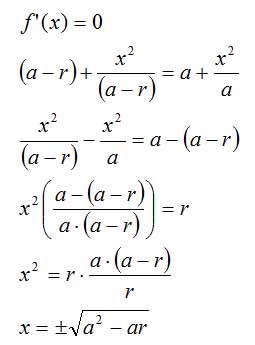
Setzt man die Werte aus der Aufgabenstellung für die Augenhöhe a = 1,78 m und für die Rocksaumhöhe r = 0,6 m ein, erhält man x = ± 1,449 m.
Der negative Wert ist in diesem Zusammenhang nicht sinnvoll, weil der Student kein Janus ist und nur in die positiv definierte Richtung blickt.
Betrachten wir zum Schluss noch kurz die Veränderung des maximalen Blickwinkels (schwarzer Punkt) in Abhängigkeit der Parameter Rocksaum- und Augenhöhe, stellen wir fest, dass kleine Menschen im Vorteil sind: Der maximale Blickwinkel ist größer und liegt bei geringeren Entfernungen!