3.2 Funções de uma variável

Uma função é uma lei que associa cada elemento em um conjunto exatamente a um elemento , em um conjunto .

Em geral consideramos as funções para as quais D e E são conjuntos de números reais. O conjunto D é chamado domínio da função. O número f(x) é o valor de f em x e deve ser lido como "f de x". A imagem de f é o conjunto de todos os valores possíveis de f(x) para quando x varia para todo o domínio. O símbolo que representa um número arbitrário no domínio de uma função f é denominado variável independente, e o que representa um número qualquer na imagem de f é chamado de variável dependente.

A) O perímetro () de um quadrado é função do comprimento do lado, isto é, . B) A distância percorrida () depende do tempo gasto (). Representamos por .

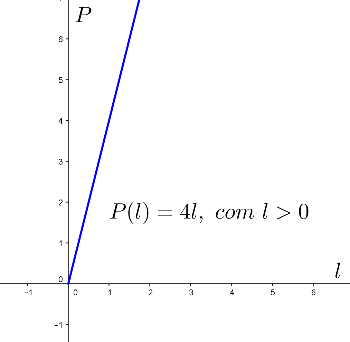
Na Educação Básica e no Cálculo 1 trabalhamos com funções de uma variável. Porém, de acordo com Stewart (2010, p. 814), "no mundo real quantidades físicas frequentemente dependem de duas ou mais variáveis."