Obersumme,Untersumme und Integral

Integralrechnung: Grundlagen und Summenregel

Ich zeige euch heut, was es mit der Summenregel der Integralrechnung auf sich hat. Unser Ziel ist es, dass wir uns die Fläche unter einer Funktion berechnen können. Zu Beginn schauen wir uns die Untersumme an. Betrachtet die folgende Grafik (f(x) = x/4 + 2,5): 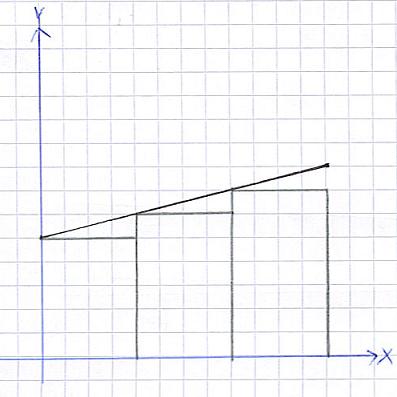Untersumme: Mit der schwarzen Linie wird die Funktion dargestellt. Damit wir uns die Fläche unter Funktion ausrechnen können, wird die Fläche in Rechtecke eingeteilt (hier mit der Breite von 2 cm). Die Flächenformel für ein Rechteck kennen wir: Länge mal Breite. Wir rechnen uns die Fläche aller Rechtecke aus und addieren diese. Wie ihr aber seht, fehlt ein kleines Stück zwischen der Fläche der Rechtecke und der Fläche der Funktion. Somit sind wir mit der Berechnung der Untersumme fertig. Obersumme: Die Vorgehensweise ist sehr ähnlich zur Untersumme. 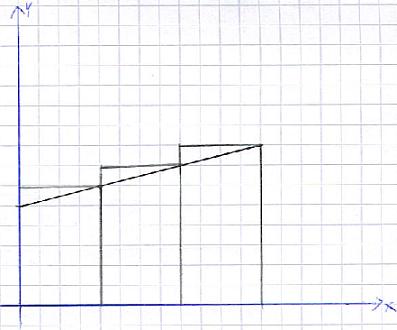Dieses mal werden die Rechtecke aber größer gezeichnet (siehe Grafik): Hier ist die Vorgehensweise wieder wie zuvor. Die Flächen der einzelnen Rechtecke werden ausgerechnet und dann addiert. Hier fällt auf, dass der Flächeninhalt größer ist als jener der Funktion. Somit hat die Untersumme eine Fläche geliefert, die zu klein ist. Die Obersumme hingegen hat eine Fläche geliefert, die zu groß ist. Exakte Fläche bestimmen: Das exakte Ergebnis für den Flächeninhalt liegt also zwischen der Untersumme und der Obersumme. Um ein richtiges Ergebnis zu bekommen, müssen wir also mehr Rechtecke einzeichnen. Je mehr Rechtecke ihr habt, desto kleiner sind die fehlenden Flächen beziehungsweise die Flächen, die zu groß sind. Ihr nähert euch damit dem "realen" Verlauf der Funktion an. Habt ihr praktisch unendlich viele Rechtecke, erhaltet ihr das Intergral! Integral: Berechnung der Fläche zwischen einem Graphen und der x - Achse.