Congruência de triângulos
Congruência de triângulos
Temos que dois triângulos são congruentes: Quando seus elementos (lados e ângulos) determinam a congruência entre os triângulos. Quando dois triângulos determinam a congruência entre seus elementos.
Casos de congruência:
1º LAL (lado, ângulo, lado): dois lados congruentes e ângulos formados por esses dois lados também congruentes.
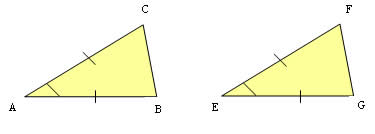
2º LLL (lado, lado, lado): três lados congruentes.
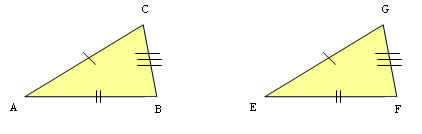
3º ALA (ângulo, lado, ângulo): dois ângulos congruentes e lado entre os ângulos congruente.
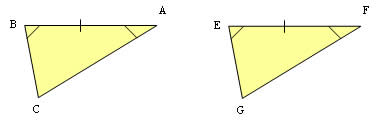
4º LAA (lado, ângulo, ângulo): congruência do ângulo adjacente ao lado, e congruência do ângulo oposto ao lado.
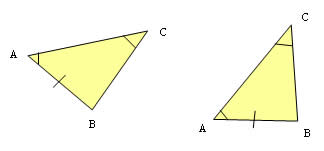
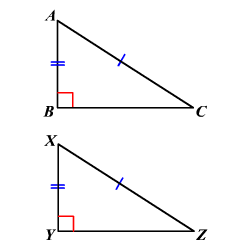
5º Caso especial de congruência de triângulos retângulos:se dois triângulos retângulos têm ordenadamente congruentes um cateto e a hipotenusa, então esses triângulos são congruentes.
Através das definições de congruência de triângulos podemos chegar às
propriedades geométricas sem a necessidade de efetuar medidas. A esse
método damos o nome de demonstração.
Dizemos que, em todo triângulo isósceles, os ângulos opostos aos lados
congruentes são congruentes. Os ângulos da base de um triângulo
isósceles são congruentes.