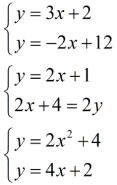Yhtälöparin ratkaiseminen
Tässä työkirjassa tutustutaan yhtälöparin ratkaisuun kahdella tavalla. Ensin katsotaan, miltä kahden ensimmäisen asteen yhtälön yhtälöparin ratkaisu näyttää koordinaatistossa. Sitten ratkaistaan yhtälöpareja CAS-laskennan avulla.
Kertaus: Suoran yhtälö ja suoran yhtälön toteutuminen
Suoran yhtälö on yhtälö, jossa esiintyvät x ja y eikä kummallakaan ole eksponenttia.
Esimerkiksi
Yhtälöt ja ja ovat suoran yhtälöitä.
Suoran yhtälön voi aina muokata ratkaistuun muotoon, jossa vasemmalla on tasan yksi y.
Esimerkiksi
on jo ratkaistussa muodossa. Toiset yhtälöt ovat ratkaistussa muodossa ja .
Harjoitus
Muuta appletissa suoran kulmakerrointa (k) ja vakiota (b) liukusäätimien avulla.
Palauta mieleen miten k:n ja b:n muuttaminen muuttaa suoran yhtälön kuvaajaa.
Jokainen suoralla oleva piste toteuttaa suoran yhtälön. Piirrä yläpuolella olevassa appletissa suora . Piste (2,3) on kuvan mukaan suoralla. Se toteuttaa suoran yhtälön.
Esimerkiksi
on suoran yhtälö ja piste (2,3) on suoralla. Sijoitetaan koordinaatit suoran yhtälöön.
Pisteen koordinaatit toteuttavat suoran yhtälön, joten tiedetään, että piste on suoralla.
Piste (3,2) ei ole suoralla. Jos sen koordinaatit sijoitetaan suoran yhtälöön, saadaan
Huomataan, että koordinaatit eivät toteuta suoran yhtälöä, joten piste ei ole suoralla.
Harjoitus
Tutki alla olevassa appletissa ovatko pisteet (1,8), (0,5) ja (−2, 2) suoralla y = 2x + 6.
CAS-ikkunaan on jo valmiiksi määritelty suoran yhtälö y = 2x + 6 ja se on piirretty oikealla. Seuraavalla rivillä on jo valmiiksi sijoitettu arvo x=1 yhtälöön f.
Komento
"Sijoita[f,x=1]"
tarkoittaa
"sijoita yhtälöön nimeltä f muuttujan x paikalle arvo 1".
a) Päättele onko laskun mukaan piste (1,8) suoralla. Entä kuvan mukaan?
b) Tutki samalla tavalla, ovatko pisteet (0,5), (−2, 2) ja (−27, −46) suoralla.
Yhtälöparin graafinen ratkaisu
Yhtälöparissa on kaksi yhtälöä. Yhtälöparin ratkaisu on sellaiset muuttujan arvot, jotka toteuttavat molemmat yhtälöt.
Tyypillisesti käsiteltävä tilanne on sellainen, jossa on kaksi suoran yhtälöä. Silloin muuttujat ovat x ja y. Tilanteen voi tulkita koordinaatistossa suorien leikkauspisteeksi. Vain leikkauspiste on molemmilla suorilla eli toteuttaa molemmat yhtälöt.
Esimerkiksi
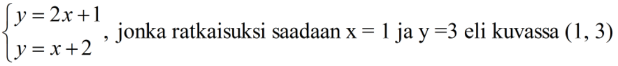
Harjoitus
Tutki yllä olevan appletin avulla, missä pisteessä leikkaavat suorat
a) y = 2x + 2 ja y = x + 2
b) y = 2x − 1 ja y = −x + 2
c) y = 3x −2 ja y = 0,5x + 3
Harjoitus
Yleisimmin käsitellään suoria, mutta kaikki leikkauspisteet ovat leikkauspisteessä kohtaavien suorien tai käyrien muodostamien yhtälöparien ratkaisuja.
Tutki alla olevassa kuvassa, minkä yhtälöparin ratkaisuna saadaan pisteiden
a) A
b) B ja C
c) D ja E
koordinaatit.
Yhtälöparin algebrallinen ratkaisu CAS-laskennalla
Yhtälöparin ratkaiseminen CAS-laskennalla on mahdollista tarkasti tai numeerisesti. Tarkan ratkaisun komento on Ratkaise. Se antaa pisteen koordinaatit kokonaislukuna, murtolukuna tai juurina. Numeerisen ratkaisun komento on RatkaiseNumeerisesti. Se antaa likiarvon silloin, kun vastauksessa on monta desimaalia.
Kummallekin komennolle pitää kertoa, minkä yhtälön tai mitkä yhtälöt haluat ratkaista. Alla appletissa on syötetty valmiiksi suorien ja paraabelien yhtälöt riveille 1-4. Komennossa riviin viitataan $-merkin avulla.
Valmiiksi kirjoitettu merkintä
Ratkaise[{$1,$2},{x,y}]
tarkoittaa siis
"ratkaise riveillä 1 ja 2 olevista yhtälöistä muuttujat x ja y".
Toisin sanoen on ratkaistu rivien 1 ja 2 muodostama yhtälöpari. Vastauksena saadaan yhtälöiden kuvaajien leikkauspiste, jonka voit tarkistaa myös edellisestä kuvasta.
Harjoitus
Kirjoita applettiin soveltuvat komennot ja ratkaise myös
a) pisteiden B ja C
b) pisteiden D ja E
koordinaatit.
Jos käytät RatkaiseNumeerisesti -komentoa ja vastaus on hyvin epätarkka, voit klikata vastausta ja näet tarkemmat lukuarvot.
Tarkasta edellisen appletin kuvasta, että vastaukset ovat järkevät.
Harjoittele lisää
Avaa Geogebra-työpöytäsovellus tai käynnistä Geogebra verkkosivulla. Tutki graafinen laskin -näkymässä ja CAS-laskimella, mitkä ovat ao. yhtälöparien ratkaisut.