FUNCIONES TRIGONOMÉTRICAS
SENO
La función asocia a cada número real, x, el valor del seno del ángulo cuya medida en radianes es x.
f(x) = sen x
Ejemplo: Estudia la siguiente función
y = sen (5x)
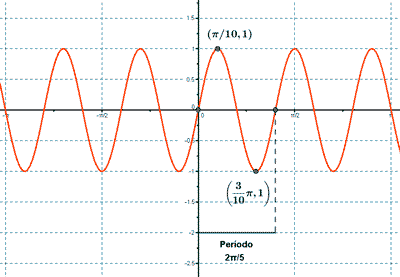1) Dominio: Dom(f) = R
2) Recorrido: Im(f) = [-1 , 1]
3) Periodicidad:
Como la función seno es periódica de período 2π, la función f(x) = sen (5x) es periódica de período:
2π = 5x ⇔ x = 2π/5
Es periódica de período 2π/5 .
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = sen 0 ⇒ y = 0 ⇒ (0 , 0)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = sen (5x) ⇒ 5x = 0 ó 5x = π ⇒ x = 0 ó x = π/5 ⇒ (0 , 0) , (π/5 , 0)
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
1 = sen (5x) ⇒ 5x = π/2 ⇒ x = π/10 ⇒ (π/10 , 1)
Los puntos mínimos de la función vendrán dados por la ecuación:
-1 = sen (5x) ⇒ 5x = 3π/2 ⇒ x = 3π/10 ⇒ (3π/10 , -1)
Ejemplo 2:
COSENO
La función coseno asocia a cada número real, x, el valor del coseno del ángulo cuya medida en radianes es x.
f(x) = cosen x
Ejemplo: Estudia la siguiente función
y = 2 cos(x)
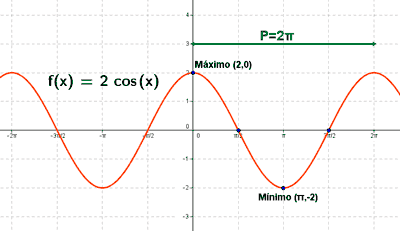1) Dominio: Dom(f) = R
2) Recorrido: Im(f) = [-2 , 2]
3) Periodicidad:
Como la función coseno es periódica de período 2π , la función f(x) = 2 cos(x) tiene el mismo período: 2π .
También podemos sacar el período de la función así:
f(x) = 2 cos(x) = 2 cos(x + 2π) = f(x + 2π)
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 2 cos 0 ⇒ y = 2 ⇒ (0 , 2)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 2 cos(x) ⇒ cos(x) = 0 ⇒ x = π/2 ó x = 3π/2
Luego los puntos de corte con el eje X son: (π/2 , 0) , (3π/2 , 0)
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
2 = 2 cos(x) ⇒ 1 = cos(x) ⇒ x = 0 ó x = 2π ⇒ (0 , 2) , (2π , 2)
Los puntos mínimos de la función vendrán dados por la ecuación:
-2 = 2 cos(x) ⇒ -1 = cos(x) ⇒ x = π ⇒ (π , -2)
Ejemplo: Estudia la siguiente función
y = 2 cos(x)
1) Dominio: Dom(f) = R
2) Recorrido: Im(f) = [-2 , 2]
3) Periodicidad:
Como la función coseno es periódica de período 2π , la función f(x) = 2 cos(x) tiene el mismo período: 2π .
También podemos sacar el período de la función así:
f(x) = 2 cos(x) = 2 cos(x + 2π) = f(x + 2π)
4) Puntos de corte:
Calculamos los puntos de corte que hayan dentro del primer período de nuestra función.
Puntos de corte con el eje Y:
Si x = 0 ⇒ y = 2 cos 0 ⇒ y = 2 ⇒ (0 , 2)
Puntos de corte con el eje X:
Si y = 0 ⇒ 0 = 2 cos(x) ⇒ cos(x) = 0 ⇒ x = π/2 ó x = 3π/2
Luego los puntos de corte con el eje X son: (π/2 , 0) , (3π/2 , 0)
5) Máximos y mínimos:
Calculamos los máximos y mínimos que se encuentran dentro del primer período de la función.
Los puntos máximos de la función vendrán dados por la ecuación:
2 = 2 cos(x) ⇒ 1 = cos(x) ⇒ x = 0 ó x = 2π ⇒ (0 , 2) , (2π , 2)
Los puntos mínimos de la función vendrán dados por la ecuación:
-2 = 2 cos(x) ⇒ -1 = cos(x) ⇒ x = π ⇒ (π , -2)Ejemplo 2:
TANGENTE
La función tangente asocia a cada número real, x, el valor de la tangente del ángulo cuya medida en radianes es x.
f(x) = tg x
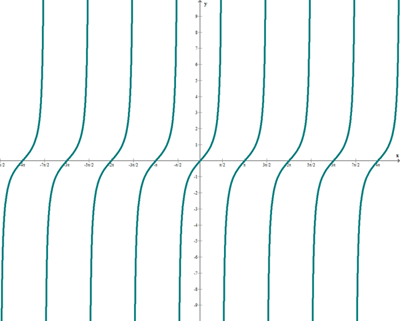Ejemplo: Estudia la siguiente función
y = tg(x/4)
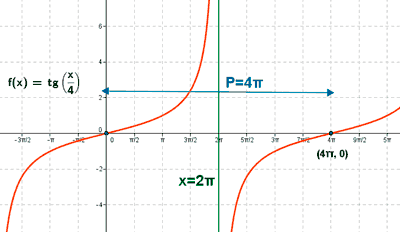1) Dominio:
La función tangente no está definida en: (2k + 1)π/2 , k ∈ Z
Por tanto, nuestra función tampoco estará definida en:
x/4 = (2k + 1)π/2 k ∈ Z ⇔ x = 2(2k + 1)π , k ∈ Z
Luego: Dom(f) = R - { 2(2k + 1)π | k ∈ Z }
2) Recorrido: Im(f) = R
3) Periodicidad:
Como la función tangente es periódica de período π , la función f(x) = tg (x/4) es periódica de período:
x/4 = π ⇔ x = 4π
Es periódica de período 4π .
4) Puntos de corte:
Puntos de corte con el eje Y:
x = 0 ⇒ y = tg(x/4) ⇒ y = tg(0) ⇒ y = 0 ⇒ (0 , 0)
Sabemos que la función tangente corta al eje X en: 0 = tg(x) ⇔ x = 0 ó x = π
En nuestro caso: 0 = tg(x/4) ⇔ x = 0 ó x/4 = π ⇔ x = 0 ó x = 4π
Como el período de nuestra función es 4π , los puntos de corte con el eje X en el primer período son: (0 , 0) , (4π, 0)
5) Máximos y mínimos:
La función tangente no tiene máximos ni mínimos, por tanto, f(x) = tg(x/4) tampoco los tiene.
Ejemplo: Estudia la siguiente función
y = tg(x/4)
1) Dominio:
La función tangente no está definida en: (2k + 1)π/2 , k ∈ Z
Por tanto, nuestra función tampoco estará definida en:
x/4 = (2k + 1)π/2 k ∈ Z ⇔ x = 2(2k + 1)π , k ∈ Z
Luego: Dom(f) = R - { 2(2k + 1)π | k ∈ Z }
2) Recorrido: Im(f) = R
3) Periodicidad:
Como la función tangente es periódica de período π , la función f(x) = tg (x/4) es periódica de período:
x/4 = π ⇔ x = 4π
Es periódica de período 4π .
4) Puntos de corte:
Puntos de corte con el eje Y:
x = 0 ⇒ y = tg(x/4) ⇒ y = tg(0) ⇒ y = 0 ⇒ (0 , 0)
Sabemos que la función tangente corta al eje X en: 0 = tg(x) ⇔ x = 0 ó x = π
En nuestro caso: 0 = tg(x/4) ⇔ x = 0 ó x/4 = π ⇔ x = 0 ó x = 4π
Como el período de nuestra función es 4π , los puntos de corte con el eje X en el primer período son: (0 , 0) , (4π, 0)
5) Máximos y mínimos:
La función tangente no tiene máximos ni mínimos, por tanto, f(x) = tg(x/4) tampoco los tiene.