Umgang mit Gleichungen im GeoGebra-CAS
Vorab eine Warnung! Zu vielen Fehlern und unerwartetem Verhalten führt das Vergessen des Malzeichens! Zwar ist GeoGebra recht flexibel und kann mit Ausdrücken wie umgehen. Will man aber zwei Variablen bzw. Parameter genauso hintereinander eingeben, wie etwa , so wird dies nicht als Produkt verstanden sondern als eine einzige Variable mit dem Namen . Deshalb sollte man gerade im CAS zur Sicherheit lieber einmal zuviel das Malzeichen "*" verwenden!
Eingabe von Gleichungen bzw. Funktionen
Man muss bei der Eingabe auf folgende Unterschiede achten: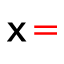 bzw.
bzw.  ... mit Textbefehlen
... mit Textbefehlen
 ... mit dem Textbefehl
... mit dem Textbefehl
- Eingabe von Gleichung mit einfachem = z.B. ... ergibt hier eine einfache lineare Gleichung, kann natürlich auch andere mathematischen Funktionen enthalten (sin, exp, sqrt, ...)
- Definition von z.B. einer Funktion mit := ... Bestimmung einer Funktion mit Parametern. Das ist in der Eingabezeile nicht möglich, ohne das ein Schieberegler bestimmt wird.
- Benennung eines Objektes über name: ... es wird eine Gleichung mit dem Namen s erstellt, bei der es darum geht, für welche x die Funktion f(x) den Wert 3 hat!
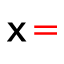 bzw.
bzw.  ... mit Textbefehlen
... mit Textbefehlen
- Löse[] oder Lösungen[ ] um eine Lösung für eine Gleichung oder ein System von Gleichungen symbolisch über den reellen Zahlen zu finden.
- NLöse[ ] oder NLösungen[ ] um numerische Lösungen der angegebenen Gleichung(en) für die Variable x zu finden.
- KLöse[ ] für Komplexe Lösungen.
 ... mit dem Textbefehl
... mit dem Textbefehl
- Ersetze[ ] kann man nachträgliche Änderung besser vornehmen. ... der Link führt wieder auf das GeoGebra-Hilfe-Wiki
(3x+2=8)-2(3x=6)/3- Ergebnis:
x=2
g1:3x+2=8. Dann könnte man auch g1/2 eingeben. Das erspart eventuell viel Schreibarbeit und ist auf jeden Fall auch dynamisch, für den Fall, dass man die Gleichung verändert!
Gleichungssystem lösen lassen
Nehmen wir an, wir haben zwei Geraden g1 und g2 definiert. Mit
Löse[{g1,g2}] wird die Lösung für x und y angezeigt.
Die doppelte geschweifte Klammern bei der Lösung kommen daher, dass es bei anderen Gleichungen ja zu mehreren Lösungen kommen kann. Ein solche Lösung mit zwei Lösungenpaaren von x- und y-Werten könnte dann so aussehen:
{{x=1,y=-3},{x=-5,y=2}}
Schneide[] kann zuverlässig nur bei Funktionen verwendet werden. Die Anwendung des Löse[]-Befehls um bei Funktionen den Schnittpunkt zu finden ist etwas umständlicher. Er müsste Löse[{y=f(x),y=g(x)}] lauten.
Dazu ein Beispiel als Bild:
Zugriff auf einzelne Teile einer Ausgabe
Für eine dynamische Verknüpfung zwischen den Zeilen darf man die einzelnen Ergenisse nicht von Hand abschreiben. GeoGebra bietet aber ein paar Funktionen, um auch zum Beispiel zwei Lösungen nacheinander einzeln weiter zu verarbeiten.
Gehen wir von dem obigen Beispiel mit der Parabel und der Gerade aus, so habe ich ja die Ausgabe:
Auf die erste Lösung/das erste Lösungpaar kann man zugreifen durch den Befehl Element[$3,1]
... mehr zum Befehl Element[ ] im Hilfe-Wiki.
Erklärung:
- Die Ausgabe ist wegen der geschweiften Klammern eine Liste.
- Die Liste enthält zwei Elemente, die beide Punkte sind.
- Also greife ich mit dem Befehl auf das erste Element in der Liste $3 (siehe Bild oben) zurück.
x(Element[$3,1]). Ist das Ergebnis aber eine Liste mit Listen (also geschweifte Klammern ineinander geschacheltet), so müsste müsste man zweimal den Element-Befehl verwenden!
Für die Lösungverfahren bei Gleichungssystemen muss man einen anderen Befehl benutzen. Schauen wir uns dazu ein Beispiel zum Einsetzungsverfahren an:
- Legen Sie die Geraden
g1:3x+4=2yundg2:4x-2y=1an. - Nutzen Sie zum Einsetzen den folgenden Befehl:
Ersetze[g2, 2y,LinkeSeite[g1]] - Nur wenn
- Bestimmen Sie die Lösung für die übrigbleibende Gleichung (mit
Löse[]oder per Äquivalenzumformung)
Ersetze[g2, 2y,LinkeSeite[g1]] sollte eigentlich nicht schwer zu verstehen sein, wenn man sich klar macht, dass er allgemein so verwendet wird:
Ersetze[ <Ausdruck>, <von>, <durch> ]
- In der Gleichung
g2wird der Ausdruck2ydurch die linke Seite der Gleichung g1 (hier also3x+4) ersetzt.
LinkeSeite bzw. RechteSeite kann auch beim Gleichsetzungsverfahren verwendet werden, indem man jeweils eine Seite der Gleichungen nimmt und sie zu einer neuen Gleichung zusammensetzt. Weitere Beispiel zu diesen Befehlen im Hilfe-Wiki, siehe RechteSeite[ ]
Für das Additionsverfahren braucht man diesen Befehl natürlich nicht, denn man kann einfach Gleichungen addieren, wie zum Beispiel g1+g2 nachdem man eventuell notwendige Äquivalenzumformungen vorgenommen hat.