Prismas
Na figura abaixo, temos dois planos paralelos e distintos, e , um polígono convexo R contido em e uma reta r que intercepta e , mas não R:
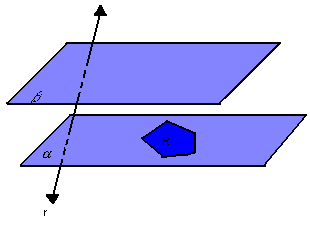
Para cada ponto P da região R, vamos considerar o segmento PP' , paralelo à reta r
(P' E ):
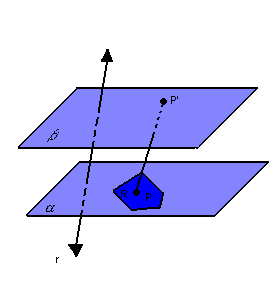
Assim, temos:
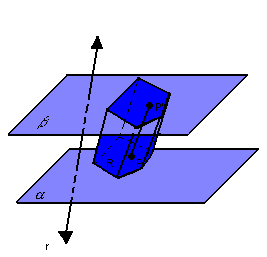
Chamamos de prisma ou prisma limitado o conjunto de todos os segmentos congruentes PP' paralelos a r
Elementos do prisma
Um prisma ilimitado convexo possui: n arestas, n diedros e n faces (que são faixas de plano).
Já um prisma convexo limitado possui:
* 2 bases congruentes (secções paralelas e distintas), n faces laterais (paralelogramos), (n+2) faces, n arestas laterais, 3n arestas, 3n diedros, 2n vértices e 2n triedros.
Classificação
Um prisma pode ser:
- reto: quando as arestas laterais são perpendiculares aos planos das bases. Num prisma reto as faces laterais são retângulos.
- oblíquo: quando as arestas laterais são oblíquas aos planos das bases.
- regular: é um prisma reto cujas bases são polígonos regulares.
Prisma reto
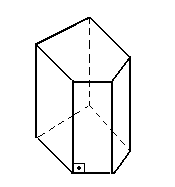
Prisma Oblíquo
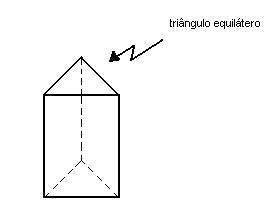
Prisma regular triangular
Prisma regular hexagonal
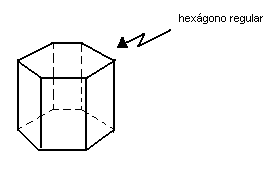
Observação: As faces de um prisma regular são retângulos congruentes.
Natureza de um Prisma
Um prisma será triangular, quadrangular, pentagonal, etc., conforme a base for um triângulo, um quadrilátero, um pentágono, etc.
Secção de Prismas
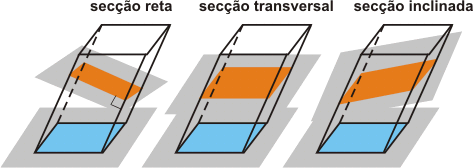
Secção é uma região poligonal plana (polígono plano) com um só vértice em cada aresta.
Secção reta ou secção normal é uma secção cujo plano é perpendicular às arestas.
Superfície de um Prisma
A superfície de um prisma ilimitado convexo é a reunião das faces desse prisma. É chamada superfície prismática convexa ilimitada ou indefinida.
Propriedades
1.ª) Secções paralelas de um prisma ilimitado são polígonos congruentes.
2.ª) A soma dos diedros de um prisma ilimitado convexo de n arestas é igual a (n-2) . 2 retos.