Justification
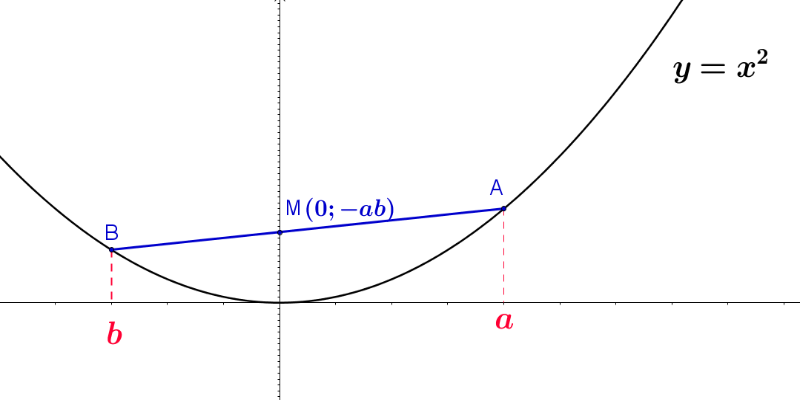
Soit A(a;a²) et B(b;b²) deux points distincts de la parabole d’équation y = x² avec a et b deux entiers tels que a > 1 et b < -1 et a ≠ b. Une équation de la droite (AB) est donnée par : Soit : Soit : y = (a + b)(x - a) + a² (comme a ≠ b) L’ordonnée du point M intersection du segment [AB] avec l’axe des ordonnées est : . Remarque : comme a et b sont de signes contraires alors -ab > 0. Comme a > 1 et b <-1, alors -ab est un entier naturel composé (il a au minimum 3 diviseurs 1; a et -ab). Lorsque a décrit tous les entiers positifs supérieurs ou égaux à 2 et b décrit tous les entiers négatifs inférieurs ou égaux à -2, alors l’ordonnée du point M décrit tous les entiers naturels composés. Donc sur l’axe des ordonnées, les ordonnées à valeur entière des points qui ne sont pas l’intersection d’une corde avec cet axe sont forcément des nombres premiers.