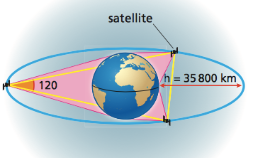
I SATELLITI GEOSTAZIONARI
LA TERZA LEGGE DI KEPLERO
La terza legge di Keplero mette in relazione le distanze dei pianeti dal Sole con i tempi di percorrenza dell'orbita: il rapporto tra il cubo del semiasse maggiore (a) e il quadrato del periodo di rivoluzione (T) è costante. Questa legge è espressa dalla formula:
Questa relazione mostra che il periodo di rivoluzione T è maggiore se a è maggiore: più un pianeta è lontano dal sole, più tempo impiega a percorrere la propria orbita.
Per ricavare questa legge, è necessario considerare che la forza centripeta , che tiene il satellite nell'orbita, è costituita dalla forza di gravità . Consideriamo un pianeta che percorre un'orbita circolare di raggio r:
Per le proprietà del moto circolare uniforme, tra il raggio orbitale r, il periodo di rivoluzione T e il modulo v della sua velocità v vale la relazione:
A destra del segno di uguaglianza, compaiono soltanto quantità costanti: G è una costante fisica universale (), la massa M è una proprietà del corpo attorno al quale orbita il pianeta o il satellite e è una costante matematica. Perciò coincide con la terza legge di Keplero. Il valore della costante K è diverso a seconda del corpo celeste attorno al quale avviene il moto orbitale perché dipende dalla massa M del corpo. Tale forma vale solo per le orbite circolari, che è stata presa in esame in relazione alla seguente trattazione dei satelliti geostazionari.
L'equazione vale per le orbite dei pianeti attorno al Sole e anche per quelle dei satelliti attorno ai pianeti. Dalla terza legge di Keplero si evince che la velocità del satellite diminuisce man mano che aumenta il raggio della sua orbita: i satelliti più lontani dal centro del pianeta impiegano più tempo per compiere un’orbita intera. Esiste un valore particolarmente interessante del raggio dell'orbita di un satellite: questo valore corrisponde a un'altezza sulla superficie terrestre di circa 35800 km.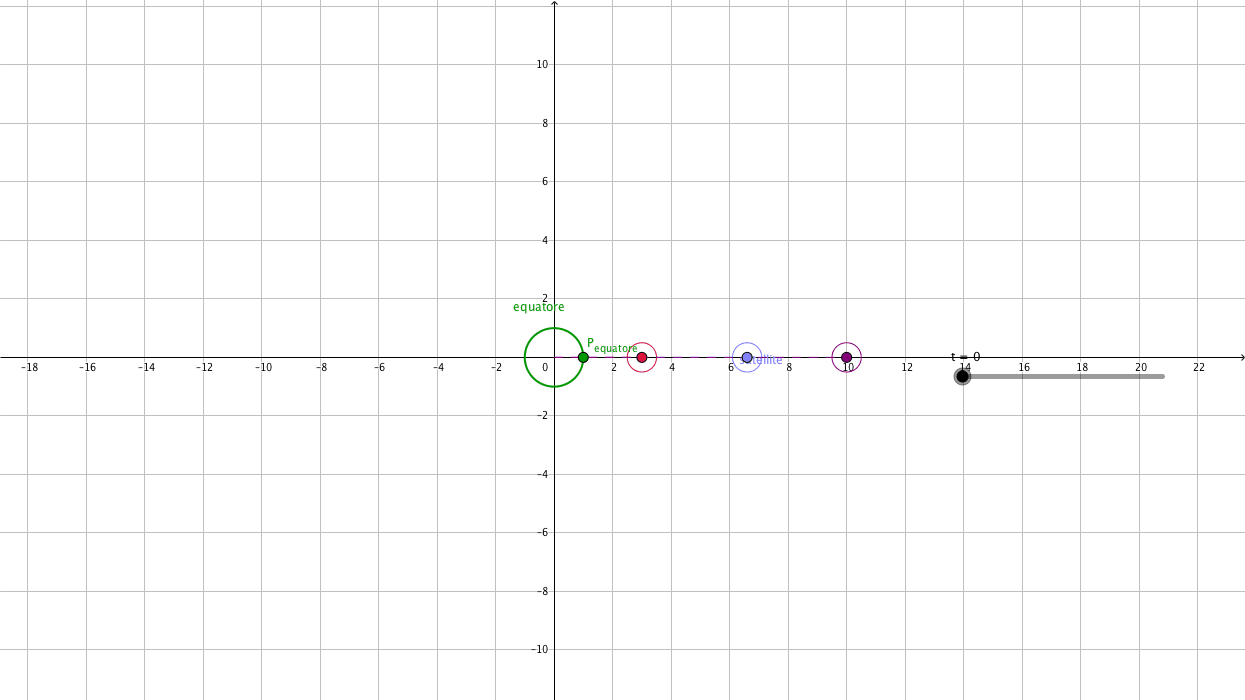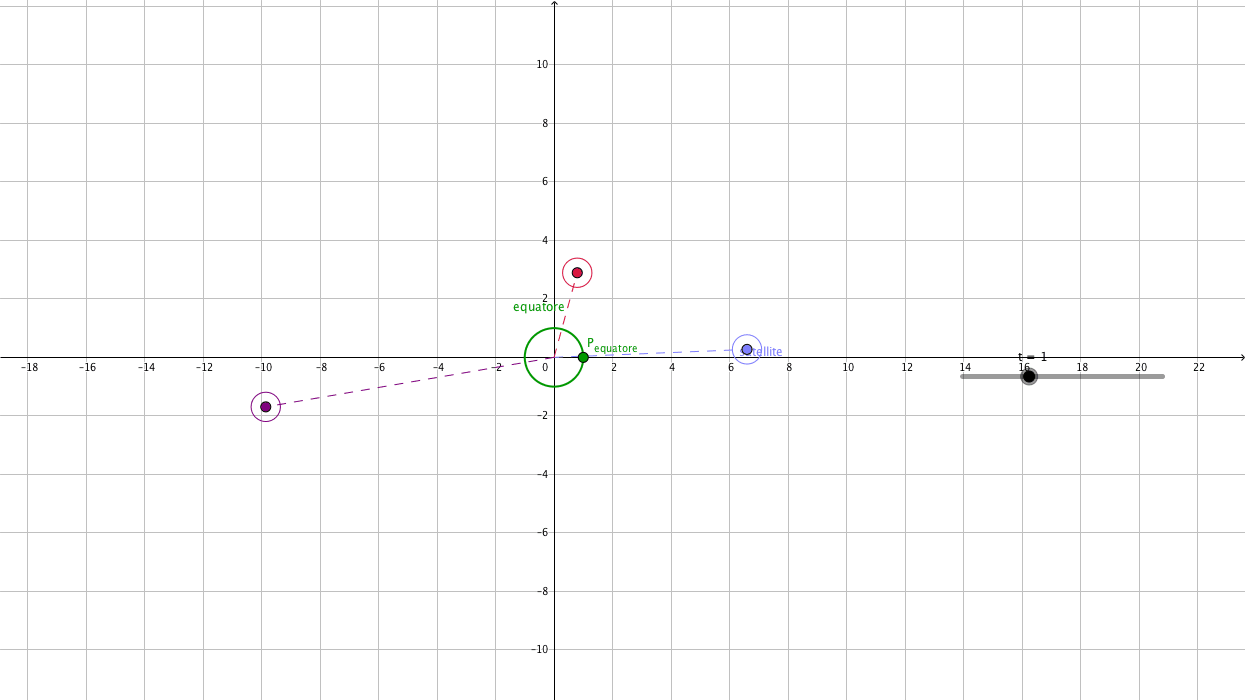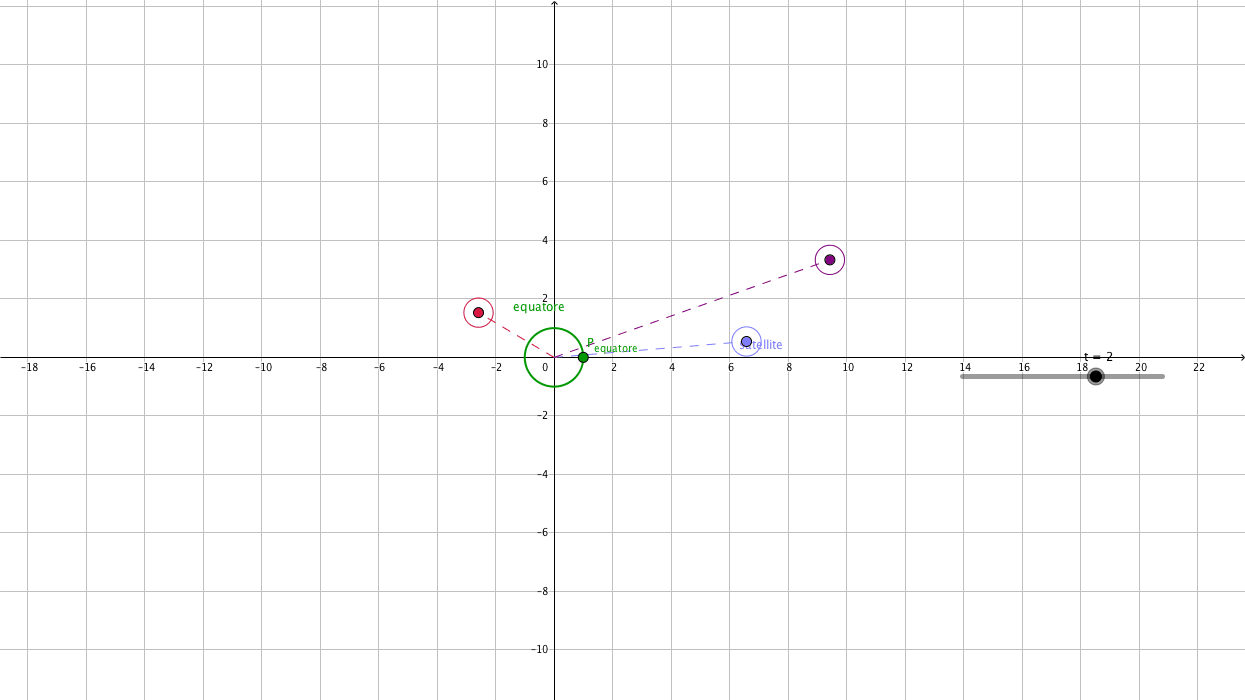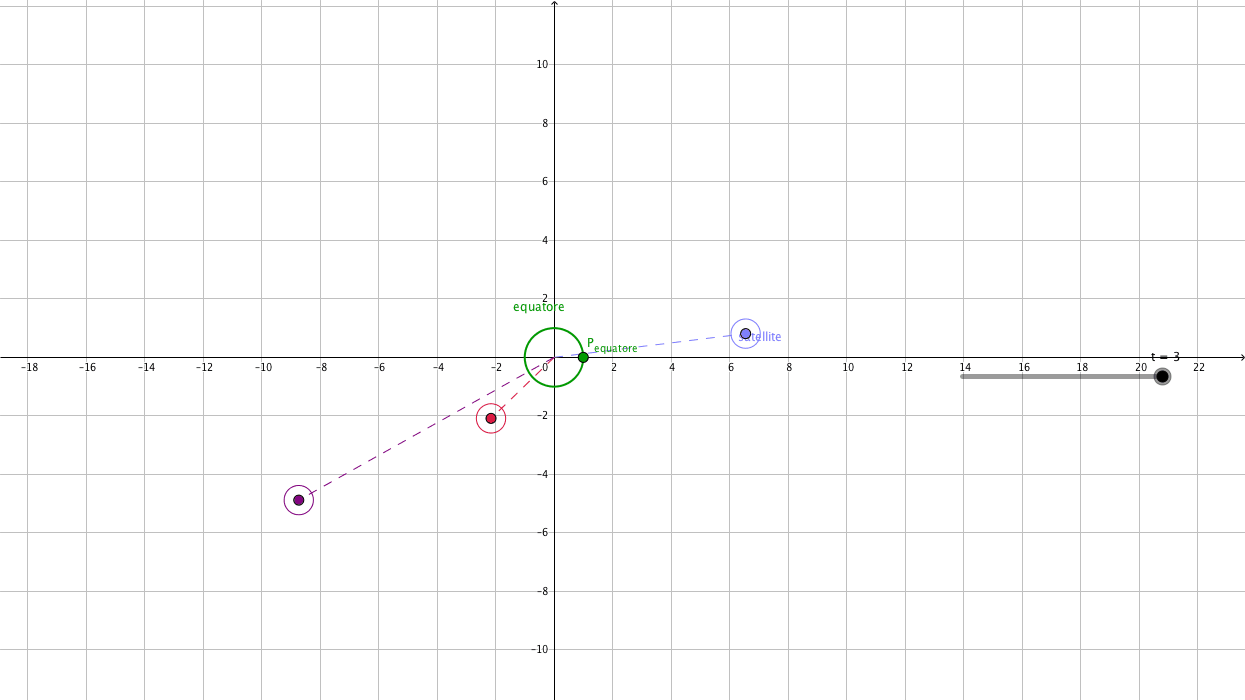
I SATELLITI GEOSTAZIONARI
Una particolare categoria di satelliti artificiali è quella dei satelliti geostazionari.
Un satellite geostazionario percorre un'orbita equatoriale circolare con un periodo di rivoluzione uguale al periodo di rotazione della Terra (23 h e 56 min); pertanto il moto relativo tra un satellite geostazionario e la superficie terrestre è nullo. Tale orbita viene, appunto, definita 'geostazionaria' in quanto per un osservatore a terra, il satellite appare fermo in cielo, sulla verticale di un punto sull'equatore.
La principale caratteristica del satellite geostazionario risulta quindi quella di muoversi alla stessa velocità angolare della Terra: .
Da questo deriva che l'accelerazione centripeta è uguale all'accelerazione di gravità .
Quest'ultima equazione ricalca proprio la terza legge di Keplero che abbiamo ricavato precedentemente.Essendo , e , allora
Al valore ricavato, bisogna poi sottrarre la lunghezza del raggio terrestre, pari a . Quindi la quota di un satellite geostazionario è uguale a . L'orbita di un satellite geostazionario deve essere circolare perché, in caso contrario, per la seconda legge di Keplero, la velocità tangenziale del satellite sarebbe maggiore quando è vicino alla Terra e minore quando è lontano da essa, quindi la velocità angolare sarebbe variabile. L'orbita del satellite è posizionata sul piano su cui giace l'equatore terrestre, perché altrimenti il satellite, pur muovendosi con la stessa velocità angolare di un meridiano, non si troverebbe sempre allo zenit di uno stesso punto della superficie terrestre. Un satellite geostazionario offre una copertura di circa un terzo della superficie terrestre. Perciò bastano tre satelliti geostazionari, posti a 120° l’uno rispetto all’altro, per inviare segnali su quasi tutta la superficie terrestre.
I satelliti geostazionari vengono utilizzati, per esempio, per le telecomunicazioni e a scopi meteorologici: il satellite meteorologico europeo Meteosat è un satellite geostazionario e, in questo modo, fotografa sempre la stessa porzione di Terra.
Beatrice Sisti