Propiedades de las potencias
La potencia representa el producto que tiene n veces el número a. El número a se llama base y el número n se llama exponente.
Ejemplo: potencias de 2:
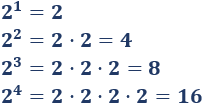
Ejemplo 2: potencias con base negativa:
Ejemplo 2: potencias con base negativa:

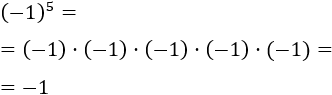
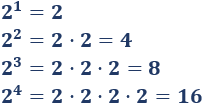
Ejemplo 2: potencias con base negativa:
Ejemplo 2: potencias con base negativa:

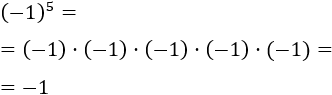
Exponente negativo
La potencia de un número distinto de 0 elevado a -1 es igual a su inverso:
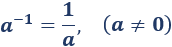
La potencia de un número distinto de 0 elevado al número negativo −n es el inverso del número elevado a n:
La potencia de un número distinto de 0 elevado al número negativo −n es el inverso del número elevado a n:
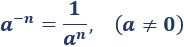
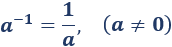
La potencia de un número distinto de 0 elevado al número negativo −n es el inverso del número elevado a n:
La potencia de un número distinto de 0 elevado al número negativo −n es el inverso del número elevado a n:
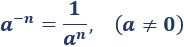
Producto y cociente de potencias
El producto de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la suma de los exponentes:
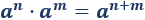
El cociente de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la resta de los exponentes:
El cociente de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la resta de los exponentes:
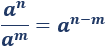
Ejemplos:
Ejemplos:
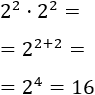
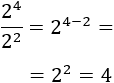
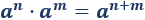
El cociente de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la resta de los exponentes:
El cociente de dos potencias con la misma base es la potencia de dicha base y cuyo exponente es la resta de los exponentes:
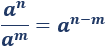
Ejemplos:
Ejemplos:
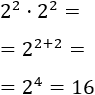
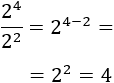
Potencia de una potencia
La potencia de una potencia con base a es la potencia con base a y cuyo exponente es el producto de los exponentes:
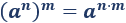
Ejemplo:
Ejemplo:
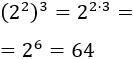
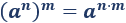
Ejemplo:
Ejemplo:
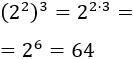
Potencia del producto y del cociente
La potencia de un producto de factores es igual al producto de las potencias de los factores:
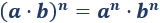
La potencia de un cociente de números es igual al cociente de las potencias de los números:
La potencia de un cociente de números es igual al cociente de las potencias de los números:
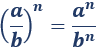
Ejemplo:
Ejemplo:
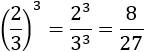
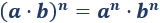
La potencia de un cociente de números es igual al cociente de las potencias de los números:
La potencia de un cociente de números es igual al cociente de las potencias de los números:
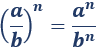
Ejemplo:
Ejemplo:
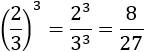
Potencia de una fracción con exponente negativo
El resultado de elevar una fracción a -1 es la fracción inversa (intercambiar el numerador y el denominador):
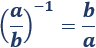
La potencia de una fracción con exponente negativo −n es la potencia del inverso de la fracción con exponente n:
La potencia de una fracción con exponente negativo −n es la potencia del inverso de la fracción con exponente n:
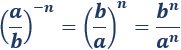
Ejemplo:
Ejemplo:
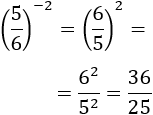
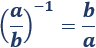
La potencia de una fracción con exponente negativo −n es la potencia del inverso de la fracción con exponente n:
La potencia de una fracción con exponente negativo −n es la potencia del inverso de la fracción con exponente n:
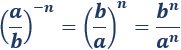
Ejemplo:
Ejemplo:
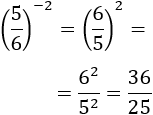
- Fracciones equivalentes y fracción irreductible
- Potencias (propiedades y ejercicios)
- Teorema de Pitágoras (con problemas resueltos)
- Ecuaciones de primer grado explicadas
- Problemas resueltos de ecuaciones
- Sistemas de ecuaciones (métodos)
- Problemas resueltos de sistemas de ecuaciones
- Ecuaciones de segundo grado resueltas
- Ecuaciones bicuadradas resueltas
- Problemas de progresiones o sucesiones
- Problemas resueltos de mcm y mcd
- Problemas resueltos de trigonometría (seno, coseno y tangente)
- Problemas de movimiento rectilíneo uniforme (MRU)
- Ecuaciones exponenciales resueltas
- Integrales resueltas (directas, por sustitución y por partes)
- Números complejos o imaginarios
- Problemas y Ecuaciones
- Logaritmos
- Teorema de Pitágoras online
- Calculadoras de porcentajes online