綱要
Teorema di Wallace-Bolyai-Gerwien
Il Teorema di Wallace-Bolyai-Gerwien (Wallace, 1806-1807(?)) e' un teorema di geometria euclidea dimostrato indipendentemente da William Wallace, Farkas Bolyai e Paul Gerwien.
Afferma che due poligoni aventi la stessa area sono sempre equiscomponibili: e' possibile tagliare il primo in un numero finito di poligoni piu' piccoli che, riarrangiati in modo diverso, formano il secondo.
La strategia della dimostrazione e' la seguente. Si osserva per prima cosa che se due poligoni sono equiscomponibili con una terza figura comune, lo sono anche tra di loro (l'equiscomponibilita' e' una relazione di equivalenza). Si dimostra quindi che un qualsiasi poligono e' equiscomponibile con un rettangolo avente una delle dimensioni di lunghezza fissa, per esempio pari a .
Siccome (a) ogni poligono e' scomponibile in un numero finito di triangoli e (b) piu' rettangoli di base possono essere impilati a formare un rettangolo piu' grande, ancora con una delle dimensioni uguale a , e' sufficiente dimostrare l'ultimo risultato per i triangoli.
I fogli geogebra illustrano i vari passi della dimostrazione:
-
[1] L'equiscomponibilità è transitiva: se due poligoni sono equiscomponibili con un terzo poligono comune, lo sono anche tra loro.
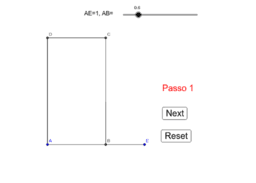
[2] Un triangolo e' equiscomponibile con rettangolo.
[3] Il rettangolo è equiscomponibile con un altro che ha uno dei lati compresi tra e . Se nessuno dei due lati del rettangolo avesse questa proprietà, possiamo decomporlo e riassemblarlo in modo da renderla vera. Infatti, se lo suddividiamo tagliando a metà uno dei lati e poi accostiamo le due parti, otteniamo un rettangolo che ha un lato dimezzato e l'altro raddoppiato. Ripetendo una o più volte questa operazione otteniamo la proprietà voluta.
[4] Infine, un rettangolo avente uno dei lati compreso tra e e' equiscomponibile con un rettangolo avente un lato uguale a