Angular Resolution
![[url=https://commons.wikimedia.org/wiki/File:Jupiter-moons.jpg]"Jupiter and Moons"[/url] by Jan Sandberg is licensed under [url=http://creativecommons.org/licenses/by/4.0]CC BY 4.0[/url]](https://www.geogebra.org/resource/H6tEVaqZ/dU3BAYB8KCvFCJKS/material-H6tEVaqZ.png)
Rayleigh's Criterion
In this picture are Jupiter and its four Galilean moons. It has many others, but they are not easy to see. Jupiter is a very bright point of light in the night sky, and if you are very lucky and conditions are just right, you might catch a glimpse of its moons with your naked eye. The light from Jupiter makes it hard to see the dimmer light from its moons, but even if you blocked the planet's light you would at best, just barely see the moons. If they were closer to Jupiter (tighter orbits), or if Jupiter were farther away, you would only see the planet and no moons. You would reach the limits of the resolving power of your eyes.
The majority of the brighter stars in the night sky are actually pairs of stars (binary) or even tertiary systems. Recent evidence indicates that around 85% of all stars in the universe are binary. The trouble is that to the naked eye and even to most telescopes, they appear as single points of light. That's why it was only recently discovered that the proportion is so high.
A simple criterion to determine whether two objects of known angular separation are resolvable by an optical device is called Rayleigh's (Ray-lees) criterion. The angular separation between the two light sources must be greater than a minimum value given by his criterion in order to be resolved. At angles less than this, the two light sources seem to melt into one. In practice the criterion is sometimes conservative, but it is easy to use, so it is widely used.
In this equation, is the wavelength of the light being observed and D is the diameter of the aperture through which the observation is being made. The angle is given in radians. For naked eye observing, D is your pupil diameter. If you use a telescope, it's the telescope tube diameter. Take note that even though your eye is at the receiving end of the telescope, that the whole job of the telescope is to increase the angular separation between objects so that you can see them, and also to collect more light than your eye would collect on its own. Your pupil is not limiting once you have a telescope to look through.
The reason we have such resolving limits is that diffraction occurs when light passes through a circular aperture. The consequence of this diffraction looks very much like a single slit pattern, except over a 2D surface. The calculation is beyond the scope of our course. In spite of this, the effect is that a sharp point of light like that from a star will diffract and produce a distribution of intensity on a screen or on film, or on your retinal surface after passing through the circular aperture. The pattern is like the one seen below. Note the similarities to the single slit diffraction that we derived. The value of tells us two things really: 1) The width (angular) of the central, bright peak due to a single, point light source, and 2) The lower limit of angular separation between two objects such that they are resolvable. The reason these two seemingly different things can be described by one and the same equation can be seen in the graphic at the end of this section. Notice that the central maximum of one of the light sources coincides with the location of the 1st minimum of the other light source when the objects are separated by
The Eyeball Complication
It turns out eyeballs have other complicating factors besides just the size of the hole (pupil) through which you look, that limit resolving power. First of all, if a person has lens defect issues that don't allow a focused image to form, then those issues will limit resolving power.
Your pupil changes size in different lighting conditions. Based on that fact alone, we'd expect to have better resolving power at night and in the dark when your pupils are dilated than during the day when your pupils are contracted. This would be consistent with Rayleigh's criterion. But this turns out to be wrong.
The down side with night vision is that the central portion of the retinal surface where our concentration tends to dwell, has virtually zero rods - the receptors used for night vision. This means that you actually have much better ability to see peripherally in the dark than straight ahead. The rod density drops to zero in the center of the retina (called the fovea). At slight peripheral angles, however, the rod (dark vision) density exceeds the cone (bright vision) density. Next time you're in the dark, pay attention to your peripheral vision. It actually works better in the dark than looking straight ahead does. This means that, for instance, detecting a dim star in the night sky is easier using peripheral vision than looking right at it. While rod receptors are much more plentiful than cones (the color receptors), they can't resolve light as well as cones. Therefore it turns out that we have better resolving power in brighter lighting conditions where cones are active in spite of our pupils being a bit contracted.
For color vision we use the cone receptors. There are special cones on the part of the retinal surface that falls on the optical principal axis. This part is called the foveola. The cone density in this region of just over 0.3 millimeter in diameter on the retinal surface contains the highest receptor packing of any receptor types on the retinal surface. In this region you have around 150,000 cone receptors per square millimeter. The foveola is completely void of rods, and also blood capillaries - because they both consume space. Oddly it is also void of S-receptors which are the short wavelength, blue light receptors. Visual acuity (resolving power by a different name) is highest in this space, but not for blue light. By about six degrees off the principal axis, or six degrees away from your point of concentration your acuity drops by around 75% for all colors. It is for this reason that we can't read well with our peripheral vision.
I want to elaborate on the blue S-receptors. Why would the eye not have blue color receptors in the foveola? The foveola is a smaller part of the fovea which as a whole is around four times larger in diameter. The fovea also has very few rod receptors, but contains S-receptors unlike the foveola. However, even then, the S-receptors are more widely spaced than the M (medium) and L (long) wavelength receptors. Why? It turns out to be the same reason that the sky is blue: Scattering. Blue light entering the eye scatters through the intraocular fluid in the eye much more strongly than red light does. It scatters so much more, that it'd be a waste to have denser packed S-receptors. Scattering smears whatever blue light images come through the pupil and lens, and therefore limits resolving power of blue light. What would be the point of having smaller or closer-packed receptors than the spots of light falling on the retina? None.
According to Rayleigh's criterion, blue light should be easier to resolve than red because it diffracts less in passing through the pupil. But the rest of the story is that there is a lower density of S-receptors and blue light gets scattered so much more, that we have about an equal ability to resolve all colors of the spectrum.
One last comment: All eyeballs are not equal. All retinas are not equal. In data I've seen, cone density in the fovea varies by around a factor of 3 among different eyeballs measured. This will certainly have an impact on resolving power. Bottom line is that pupil diameter is only one way to roughly estimate human eyeball resolving power.
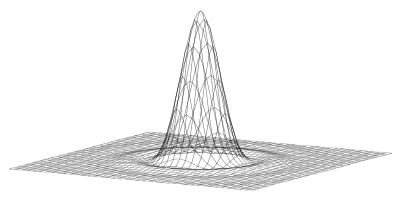
Circular Aperture Instensity Pattern
In the absence of such complicating factors, when light from two sharp sources passes a circular aperture, two blurred patterns emerge on whatever surface lies beyond. If the angular separation of the two sources is too small, the patterns can merge into what becomes one superimposed pattern. Photographs are shown below.
![[url=https://en.wikipedia.org/wiki/Angular_resolution#/media/File:Airy_disk_spacing_near_Rayleigh_criterion.png]"Airy Disk"[/url] by Spencer Bliven is in the [url=http://creativecommons.org/publicdomain/zero/1.0/]Public Domain, CC0[/url]
Two light sources starting at 2x Rayleigh's criterion in the top photo, moving closer until in the middle photo they are at Rayleigh's criterion. The bottom photo is taken with light sources at a separation of half Rayleigh's criterion. Notice how they look like a single source in the bottom case, and nearly so at the minimum angle given by Rayleigh's criterion.](https://www.geogebra.org/resource/mY67RBkM/kRF4dtmoauPsvB0i/material-mY67RBkM.png)
Try moving the sliders in the graphic below. All parameters relating to angular resolving power associated with Rayleigh's criterion are adjustable - the angular separation of the objects being viewed, the size of the aperture through which the objects are being viewed, and the light wavelength. You will see that the resulting pattern of intensity depends on all of them.