Quantum Tunneling
Imagine a classical physics scenario in which an object contains kinetic energy K. Maybe it's a ball. The ball is confined to a region of space since the ground rises uphill in all directions. The height of the hill reaches a maximum of h in all directions - maybe like the rim of a volcano where the ball is inside. It would require potential energy U=mgh to exit the volcano. In classical physics, if , the ball is trapped and will never exit the volcano on its own.
We will soon see that while this is true in the macroscopic realm, that in the quantum realm there is the possibility that a particle with energy may in fact escape such confinement. The process is called quantum tunneling - a name which alludes to the fact that the particle doesn't have energy enough to "climb the hill", but rather finds a way to tunnel through it. Please do not take the name to imply any physical act of tunneling. We don't mean hills of dirt and rock anyway. It's invisible fields that are confining the particle in a quantum sense.
Applications of quantum tunneling apply to both nuclear radioactive decay, nuclear fusion, technologies like STM (scanning tunneling microscopy) and even as we have found out recently, to myriad applications in biology. So tunneling keeps us alive in a very real sense in addition to keeping our sun burning.
Probability of Tunneling
Using Schrödinger's equation, we will now solve for the likelihood of a particle escaping through a potential energy barrier of energy and of width . We write rather than , since we simply assume inside the barrier to simplify things. Therefore . First we need to manipulate Schrödinger's equation so that we can find the form of the wave function. Starting with the usual form of the equation:
Note that unlike the particle in the box, that the two terms here have opposite signs. This means the wave function's second derivative with respect to position must be equal to a positive constant times the wave function itself. The only function that does this is the exponential. We therefore use as a trial function . Note that the constant must be zero since otherwise to the right, in the forbidden region where the amplitude of the wave function and the associated probability would rise without limit. This presents two problems: The wave function wouldn't be normalizable, and the implications would be that a particle is more likely to make it ever deeper into a forbidden region. The second problem is counter-intuitive, which doesn't mean it's necessarily wrong (since nature can sometimes be counter-intuitive), but as it turns out, experiments tell us that our intuition is indeed correct in this case.
Therefore, given a barrier where and zero otherwise, we must assume . Plugging into Schrödinger's equation and cancelling terms gives:
Using this value of , the tunneling probability to penetrate a barrier of width w, can be calculated as follows:
.
This just says that the tunneling probability is the ratio of the probability of being outside the barrier to that being inside the barrier. The meaning of this probability is exactly what it sounds like. If a particle kept bouncing around inside a box, it is making attempt after attempt at escaping. The tunneling probability is the probability that the particle succeeds. When I say "bouncing around", we should really be thinking of a reflecting traveling wave going back and forth as a wave on a guitar string.Quantum Tunneling in Biological Systems
Scanning Tunneling Microscopy
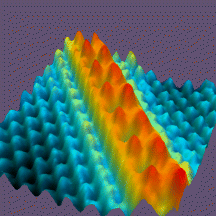
Scanning tunneling microscopes take advantage of quantum tunneling to provide atomic scale resolution in the imaging of surfaces. They do this by moving (scanning) a very fine conducting tip (typically 1 nm diameter or less) above the surface of a material. There is an induced voltage difference between the scanning tip and the sample so that electrons should want to jump the gap of vacuum between the sample and tip. The tip, however, remains too distant for the electrons to make the jump. The energy required is too large. Given the fact that tunneling probability is non-zero for such classically-forbidden jumps, there is a measurable electron current when the tip is close enough to the sample. The scanning is done such that the tip is moved so that the tunneling current remains constant during the scan. The required movement of the tip to maintain that constant tunneling current indicates the topography of the material being scanned and results in surface mappings like in the photo above. An animation of such an STM scan is seen below.
