GeoGebra

Função Quadrática

Autor:Nilson Osvaldo Gama Santa Maria

Lembrete: O que é uma função?

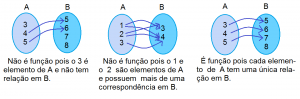
Lembrete: O que é uma função?
Sendo A e B conjuntos não vazios, uma relação F de A → B (lê-se A em B) é denominada aplicação de A – domínio, conjunto de partida – em B – contradomínio, conjunto de chegada –, ou função definida em A com imagens em B se para todo x ∈ A existe um só y ∈ B, tal que (x,y) ∈ F.

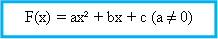
1. O que é uma função quadrática?

1. O que é uma função quadrática?
A função quadrática, ou função polinomial do segundo grau, é uma aplicação F de  →  que associa a cada x o elemento (ax² + bx + c) ∈ , em que a, b e c são números reais dados e a ≠ 0. Pois se a = 0, não teremos mais uma função quadrática e sim uma função afim: y = bx + c.

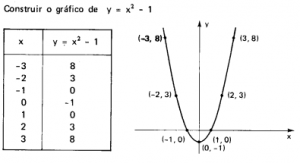
2. Gráfico

2. Gráfico
Como pôde-se perceber, na imagem acima, o gráfico da função quadrática é uma parábola.

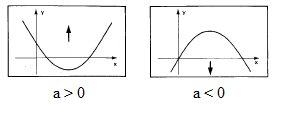
3. Concavidade

3. Concavidade
A parábola representativa da função quadrática pode ter sua concavidade voltada para cima ou para baixo. Isso dependerá do sinal de a:
  • Se a > 0, a concavidade será voltada para cima.
  • Se a < 0, a concavidade será voltada para baixo.

4. Forma Canônica

A construção do gráfico da função quadrática através de uma tabela de valores de x e de y nem sempre é precisa, pois pode acontecer que em certa função o valor da abscissa (valor de x) ou da ordenada (valor de y) não seja inteiro. Para iniciarmos um estudo mais detalhado da função, vamos transformá-la em outra forma mais adequada, chamada forma canônica.
  • Colocamos em evidência:
  • Adicionamos e subtraímos :
  • Colocamos novamente a em evidência:
Portanto, a forma canônica da função quadrática é:

5. Zeros ou Raízes

Os zeros ou raízes da função são os valores de x para os quais . Utilizando a forma canônica temos:  1. Considerando a = 0, então:    2. Mas sabemos que a ≠ 0, então:  Portanto: Observemos que, para existir raízes reais na equação do segundo grau, precisamos que seja real. Logo, temos três casos: 1. e, portanto, a equação apresentará duas raízes reais e distintas, que serão: e . 2. e, portanto, a equação apresentará duas raízes reais e iguais, que serão: . 3. e sabemos que, neste caso, , portanto, diremos que a equação não apresentará raízes reais. Interpretando geometricamente, os zeros da função quadrática são as abscissas dos pontos onde a parábola corta o eixo x.

6. Máximo e Mínimo

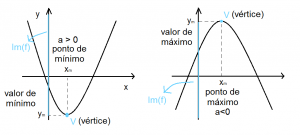
6. Máximo e Mínimo
Sendo o conjunto imagem, dizemos que  é o valor de máximo da função se, e somente se, para qualquer . E então, o número sendo o conjunto domínio, é chamado de ponto de máximo da função. Dizemos que é o valor de mínimo da função se, e somente se, para qualquer . E então, o número é chamado de ponto de mínimo da função. Sucintamente, podemos dizer que: 1. Se a < 0, a função quadrática admite o valor máximo , para . 2. Se a > 0, a função quadrática admite o valor mínimo , para .

7. Vértice da Parábola

O ponto V é chamado vértice da parábola.

Nuevos recursos

Descubrir recursos

Descubre temas