Logarithms: equations, systems and properties
1. Properties
1. Logarithm of a product
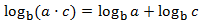
2. Logarithm of a quotient
2. Logarithm of a quotient
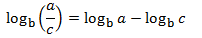
3. Logarithm of a power
3. Logarithm of a power
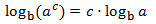
4. Change of base
4. Change of base
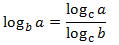
5. Inverse
5. Inverse
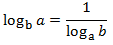
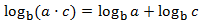
2. Logarithm of a quotient
2. Logarithm of a quotient
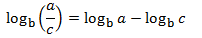
3. Logarithm of a power
3. Logarithm of a power
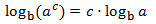
4. Change of base
4. Change of base
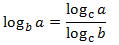
5. Inverse
5. Inverse
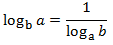
2. Equations
A logarithmic equation is an equation that has an unknown factor in the argument of a logarithm. In reality, the resolution is reduced to the resolution of equations of the same type as the expressions in the arguments (quadratic equations, cubic equations, irrational equations...).
Example 1
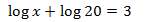 We will use the properties of logarithms and that
We will use the properties of logarithms and that
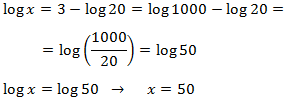
We have an equality between logarithms, so the arguments (what is inside) has to be the same:
We have an equality between logarithms, so the arguments (what is inside) has to be the same:
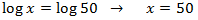
The solution to the equation is x = 50.
The solution to the equation is x = 50.
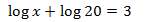 We will use the properties of logarithms and that
We will use the properties of logarithms and that
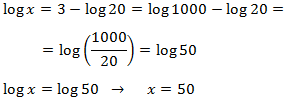
We have an equality between logarithms, so the arguments (what is inside) has to be the same:
We have an equality between logarithms, so the arguments (what is inside) has to be the same:
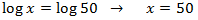
The solution to the equation is x = 50.
The solution to the equation is x = 50.Example 2
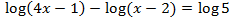
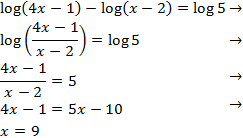
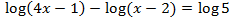
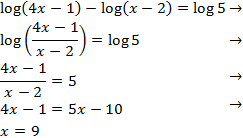
3. Logrithmic equation systems
Example 1
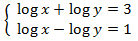
We apply the change of variable
We apply the change of variable
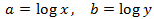
This way we obtain the following linear equation system
This way we obtain the following linear equation system
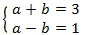
we resolve it and we undo the cange of variable:
we resolve it and we undo the cange of variable:
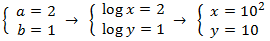
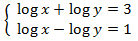
We apply the change of variable
We apply the change of variable
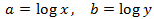
This way we obtain the following linear equation system
This way we obtain the following linear equation system
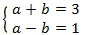
we resolve it and we undo the cange of variable:
we resolve it and we undo the cange of variable:
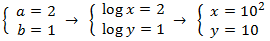
Example 2
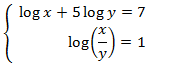
First we apply the property logarithm of a product:
First we apply the property logarithm of a product:
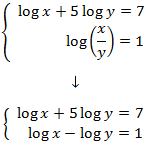
We apply the change of variable:
We apply the change of variable:
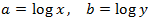
and we obtain the following system:
and we obtain the following system:
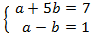
that has as solution:
that has as solution:
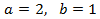
Finally, we undo the change of variable:
Finally, we undo the change of variable:
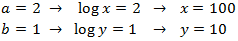
We do not need to check the solutions.
We do not need to check the solutions.
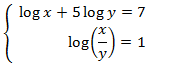
First we apply the property logarithm of a product:
First we apply the property logarithm of a product:
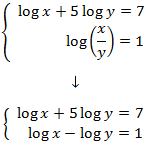
We apply the change of variable:
We apply the change of variable:
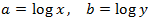
and we obtain the following system:
and we obtain the following system:
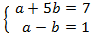
that has as solution:
that has as solution:
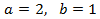
Finally, we undo the change of variable:
Finally, we undo the change of variable:
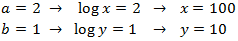
We do not need to check the solutions.
We do not need to check the solutions.More examples: