Problemas de optimización
Introducción
El cálculo diferencial básico (nivel bachillerato) nos permite resolver problemas de optimización. En estos problemas, se desea encontrar los puntos de máximos y/o mínimos de una función, es decir, se maximiza o minimiza una función.
Ejemplo de problema:
Encontrar parejas de números x e y tales que y sea el doble del cuadrado de x y que la resta de sus cuadrados () sea máxima.
La función que debe optimizarse en este problema es .
Método de resolución
Para resolver este tipo de problemas, seguiremos el siguiente esquema:
- Encontrar la función que se debe maximizar o minimizar.
- Calcular la derivada de la función .
- Igualar a 0 la derivada de para encontrar los puntos críticos (puntos candidatos para ser extremos).
- Estudiar la monotonía de la función en los intervalos que determinan los puntos críticos para determinar si son o no extremos (criterio de la primera derivada). Este paso se puede omitir si se aplica el criterio de la segunda derivada.
Ejemplo resuelto
Resolvemos el problema presentado en la introducción:
La función que debemos maximizar es .
Como, además, y debe ser el doble de x^2, tenemos que y = 2x^2. Sustituimos en la función:
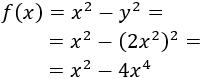
Derivamos:
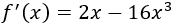
Puntos críticos:
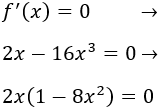
Los puntos críticos son x = 0 y
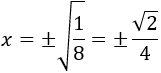
Analizando la monotonía, la función tiene máximos en los puntos
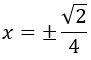
Por tanto, las parejas de números que buscamos son
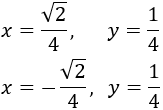Más Problemas resueltos de Optimización
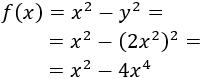
Derivamos:
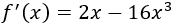
Puntos críticos:
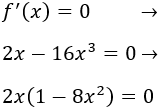
Los puntos críticos son x = 0 y
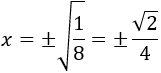
Analizando la monotonía, la función tiene máximos en los puntos
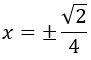
Por tanto, las parejas de números que buscamos son
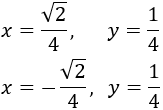Más Problemas resueltos de Optimización