Elipse. Ecuación reducida
Ecuación reducida de la elipse.
La potencia del programa nos permite rotar y trasladar la elipse para después comprobar la ecuación reducida con los parámetros medidos previamente.
| Pasos | Herramientas | Elaboración |
| Representar una elipse cualquiera. |
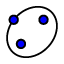 | Selecciona primero los focos y después un punto de la elipse. Focos (a,b) y (c,d) y punto (e,f). Las coordenadas suman tu número de lista. La elipse en general tendrá términos cruzados.(axy) |
| Comprobar la definición de elipse |
 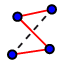 | Dibuja un punto sobre la elipse y comprueba que la suma de distancias a los dos focos se mantiene constante. |
| Hallar el centro de la elipse y sus parámetros. Dibujar sus ejes. |
     | Utiliza las herramientas de la izquierda para obtener, semieje menor y mayor, semidistancia focal, constante de la elipse y excentricidad. |
| Girar la elipse para que sus ejes sean paralelos a los ejes coordenados. |
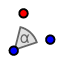 | Si a es la recta que contiene al eje mayor, hacer girar la elipse con respecto a su centro un ángulo igual a -atan(pendiente[a]). La elipse tendrá términos lineales.(ax, by). |
| Trasladar la elipse hasta el origen de coordenadas. |
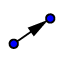  | Obtener el vector que une el Centro de la elipse con el origen y trasladar la elipse según ese vector. |
| Comprueba que los parámetros obtenidos midiendo son los que aparecen en la ecuación reducida. | ||
| Puntos seleccionados. |