Máximos y mínimos: Problemas de aplicación.
Con frecuencia en la vida, nos enfrentamos con el problema de encontrar la mejor manera de hacer algo, por ejemplo:
- Un granjero necesita elegir la mezcla de cultivos que sea la más apropiada para producir la mayor ganancia.
- Un médico desea seleccionar la menor dosis de una droga que curará cierta enfermedad.
- A un fabricante le gustaría minimizar el costo de distribución de sus productos.

Máximo y Mínimo
Para encontrar el máximo (y/o mínimo) de una función cualquiera f(x), resulta de:
- Encontrar las raíces (a) de f'(x):
- Máximo: sí al evaluar a en f''(x) < 0
- Mínimo: sí al evaluar a en f''(x) > 0
Optimización: Estrategia para resolver problemas de Máximos y Mínimos
Para los problemas de aplicación en donde se requieren encontrar los máximos y mínimos (optimización):
- Haga un dibujo del problema
- Asigne las variables idóneas para las cantidades importantes
- Escriba una función que se maximizará o minimizará, en términos de las variables
- Utilice las condiciones del problema para eliminar todas las variables. Hasta quedar en términos de una variable
- Encuentre los máximos (o mínimos) de la función
- Revise los resultados.
Problema 1
Una caja cuadrada se fabrica con una pieza de cartón de 6 cm de lado, de la cual se cortan cuadrados idénticos a partir de las cuatro esquinas y se doblan los lados hacia arriba.
Determine las dimensiones de la caja de volumen máximo. ¿Cuál es este volumen?
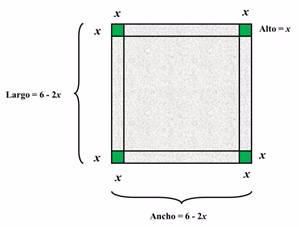
Solución
Siendo x el lado de cuadrado a recortar y V el volumen de la caja resultante. Entonces:
Dado que lo mínimo a recortar es 0 y lo máximo es 3. Entonces el volumen a maximizar está entre [0,3]. Para obtener el máximo, derivamos con respecto a la única variable: Siendo las raíces x = 3 y x = 1. ¿Cuál valor es el resultado?