Google Classroom
GeoGebraGeoGebra Classroom

Esquema

La struttura del piano cartesiano

Autor:Gae Spes
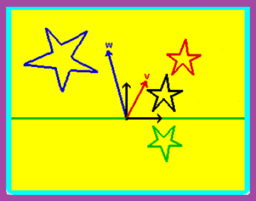
Descrizione Introduzione assiomatica del piano cartesiano (ossia come struttura basata su concetti primitivi e assiomi motivati da un modello grafico), con esplorazione delle trasformazioni più elementari, non subordinata a concetti goniometrici, bensì adatta a costituirne il fondamento; e non subordinata ad una trattazione sintetico-euclidea dei concetti geometrici coinvolti. Obiettivi - Collegare l’operazione di addizione nel piano cartesiano alle traslazioni in un piano riferito a un punto origine, e l’operazione di moltiplicazione con coefficienti reali alle omotetie in un piano riferito a un'origine e a una unità; - introdurre le isometrie coordinate in un piano riferito a un'origine, a una unità reale e a una immaginaria, individuando gli operatori di coniugazione e di ortonormalità come loro generatori - interpretare proporzioni fra punti tramite sistemi di riferimento, e l’operazione di moltiplicazione tramite roto-omotetie, isolando fra queste le rotazioni come base del concetto di modulo (distanza dall'origine) e come elementi costitutivi delle isometrie. http://w3.romascuola.net/gspes/c/ http://w3.romascuola.net/gspes/plusper.html http://tinyurl.com/geopianoc http://tinyurl.com/strupianC http://tinyurl.com/primitivic http://tinyurl.com/primitC http://tinyurl.com/teoriaxC http://tinyurl.com/ggbdaurl http://www.facebook.com/informatematica http://www.matematicamente.it/manuali-scolastici/dal-problema-al-modello-matematico-volume-1 http://www.facebook.com/photo.php?fbid=1290406017679142 L'indirizzo abbreviato del presente libro è: http://tinyurl.com/struplan oppure http://tinyurl.com/axiomaticc oppure http://tinyurl.com/gaespesc
La struttura del piano cartesiano

Tabla de contenidos

Siguiente
Gli oggetti primitivi del piano cartesiano

Nuevos recursos

Descubrir recursos

Descubre temas