Lugares geométricos 2

Autor:José Luis Soto Munguía

En la construcción siguiente (Figura 1), se han trazado dos puntos A y B a 8 unidades de distancia entre sí sobre una recta cualquiera, luego se trazó la recta BD formando un ángulo CBD con la primera, posteriormente se ha trazado la bisectriz BE al ángulo CBD y una recta paralela a BE que pasa por A. Esta paralela interseca a la recta BD en el punto P. El ángulo CBD puede abrirse y cerrarse usando el delizador k.

En el Applet siguiente se muestra la construcción dinámica de la Figura 1, arrastre el deslizador k para verificar que la construcción funciona como se ha explicado.

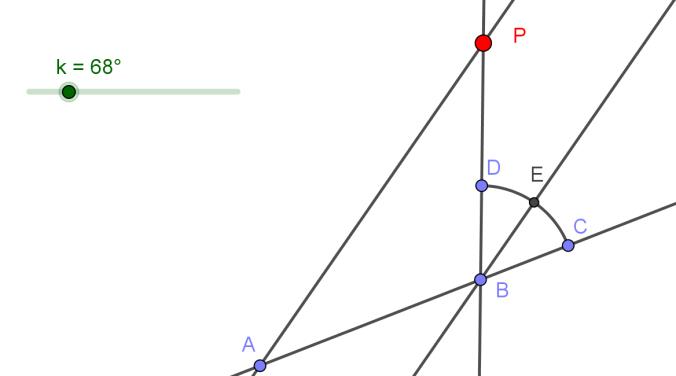
1. En el Applet anterior, arrastre el deslizador k y observe que el punto P traza una circunferencia, identifique el segmento que funciona como radio y el punto que funciona como centro de esta circunferencia y especifíque cuáles son.

2. Para justificar por qué la curva trazada es una circunferencia, basta con justificar que la magnitud del segmento identificado como radio no cambia al arrastrar k. Las siguientes preguntas le permitirán avanzar en esta justificación:

a) Identifique todos los ángulos que permanecen iguales cuando arrastra k y especifique aquí cuáles son:

b) Utilice la manera como se hicieron los trazos de la construcción, para justificar por qué los ángulos identificados son iguales.

c) ¿Qué tipo de triángulo es el ABP, a pesar del movimiento?

d) Justifique su afirmación anterior

e) Justifique ahora por qué la magnitud del segmento BP permanece constante, a pesar del movimiento.

3. El Applet siguiente es parecido al anterior, pero ahora se ha trazado una perpendicular a la recta AB, que pasa por P e interseca a la recta AB en el punto Q, por estas razones el triángulo BQP de este Applet, es rectángulo.

Arrastre k en este applet para verificar que el triángulo BQP permanece como triángulo rectángulo durante el movimiento.

a) Aplique el teorema de Pitágoras al triángulo BQP para establecer la relación entre las magnitudes s, t y BP.

b) ¿La relación encontrada en el inciso anterior se satisface, sin importar en qué posición está P? Justifique su respuesta.

c) Como todo punto P sobre la curva trazada satisface la relación encontrada, se dice entonces que esta relación es la ecuación de la curva, es decir una representación algebraica de la circunferencia. Si en lugar de haber construido un segmento AB de magnitud 8, hubiéramos partido de un segmento AB de magnitud 4, ¿cuál sería la ecuación de la circunferencia?

Lugares geométricos 2

Nuevos recursos

Descubrir recursos

Descubre temas