Función de proporcionalidad inversa
Su expresión general es  con
con  Para dibujarla es conveniente tomar para “x” divisores de k (para evitar decimales) y además está prohibido poner el cero en lugar de “x”.
Para dibujarla es conveniente tomar para “x” divisores de k (para evitar decimales) y además está prohibido poner el cero en lugar de “x”.
- El dominio es R-{0}. Su gráfica se llama hipérbola.
- El recorrido es R-{0}
- La función presenta una discontinuidad de salto infinito en x=0.
- No corta a los ejes de coordenadas.
- La recta x=0 es una asíntota vertical
- La recta y=0 es una asíntota horizontal
- Tiene simetría impar (respecto al origen de coordenadas).
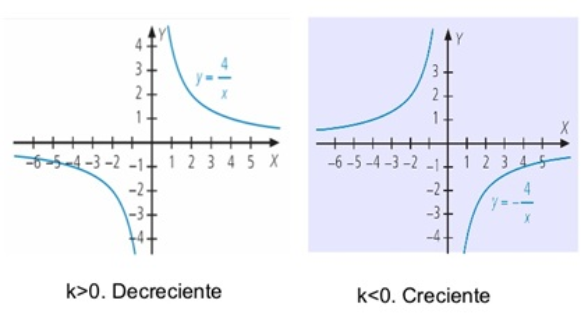
- Si k>0, la función es decreciente y su gráfica está en el 1º y 3º cuadrante. La curva es cóncava en
( y convexa en
- Si k<0, la función es creciente y su gráfica está en el 2º y 4º cuadrante. La curva es convexa en
y cóncava en
Aplicaciones de la función de proporcionalidad inversa
La función de proporcionalidad inversa aparece en numerosos fenómenos físicos y sociales. Algunos casos comunes ilustrativos de la aplicación de esta función serían:
- La relación entre la presión y el volumen en un gas ideal sometido a una temperatura k constante, que sigue el principio conocido como ley de Boyle-Mariotte: P·V=k . En este caso, el dominio de definición se restringe a la rama positiva de la función de proporcionalidad inversa, ya que no existen volúmenes ni presiones negativos.
- La relación entre el caudal de un grifo y el tiempo que tarda en llenar un depósito de una capacidad determinada.
- La relación entre la intensidad de corriente y la resistencia eléctrica en una porción de circuito sometida a una diferencia de potencial constante, como consecuencia de la ley de Ohm: V=I·R
- La intensidad y la resistencia se hallan en relación de proporcionalidad inversa.
- La relación entre el número de pacientes que asiste a una consulta médica de horario limitado y el tiempo que puede dedicar el médico a cada paciente.
Ejercicio:
Según la Ley de Boyle-Mariotte, la presión que ejerce un gas y el volumen que ocupa son inversamente
proporcionales. A 25ºC, determinada cantidad de gas, ocupa un volumen de 2 litros y ejerce una presión de 3 atmósferas.
a) ¿Qué volumen ocupará cuando la presión ejercida sea de 1 atmósfera?
b) ¿Qué presión ejercerá cuando el volumen sea de 3 litros?
c) Escribe la función presión – volumen y dibuja su gráfica.