Decoratie
Je kunt het Alhambra in Granada bezoeken vanuit een interesse in kunst, een interesse in geschiedenis, een interesse in wiskunde...
Op welke manier je het ook bezoekt, je wordt gegarandeerd omvergeblazen door de fabelachtige decoratie. Van de herhaling van een eenvoudige motiefje tot ingenieus in elkaar vervlochten patronen met spiegelingen en draaiingen, telkens is het resultaat weer net iets anders dan in de vorige zaal.
In dit GeoGebraboek onderzoeken we hoe deze patronen opgebouwd worden

Behangpapierpatronen
De wandbedekkende patronen noemen we behangpapierpatronen.
De patronen vertrekken telkens vanuit een basismotief waarop een of meerdere transformaties worden toegepast. Deze transformaties zijn: verschuiving, spiegeling, glijspiegeling en draaiing.
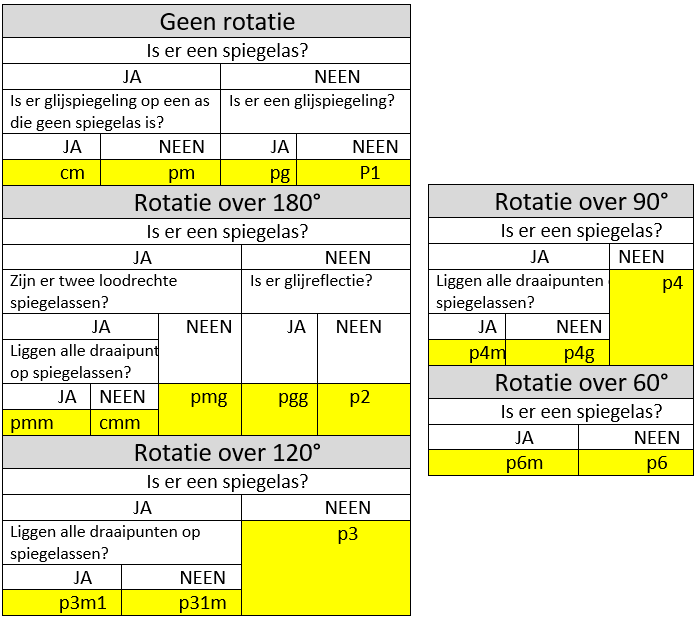
Behangpatroongroepen
Wiskundige bogen zich over verschillen en gelijkenissen tussen deze patronen en deelden ze in 17 groepen in.
Elke groep wordt bepaald door een combinatie van de toegepaste transformaties. In de volgende hoofdstukken bekijken we de verschillende groepen. Om de aard van de transformaties schematisch voor te stellen, gebruiken we volgende legende:

Zo wordt in onderstaand voorbeeld het basismotief omschreven door de gele rechthoekige driehoek links onderaan.
De driehoek wordt horizontaal en een verticaal gespiegeld tot een basisruit (of een vierkant wanneer de driehoek gelijkbenig is). Deze basisruit wordt telkens herhaald in een wandbedekkend patroon.
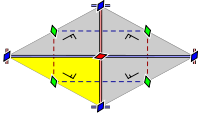
Een voorbeeld van dit patroon vinden we in het Alhambra als: