Sucesiones acotadas
Conceptos
Una sucesión a(n) es acotada superiormente cuando ninguno de sus términos es mayor que algún número K:
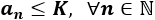 Una sucesión a(n) es acotada inferiormente cuando ninguno de sus términos es menor que algún número K:
Una sucesión a(n) es acotada inferiormente cuando ninguno de sus términos es menor que algún número K:
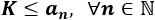 Una sucesión a(n) es acotada cuando es acotada superior e inferiormente:
Una sucesión a(n) es acotada cuando es acotada superior e inferiormente:
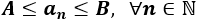
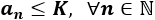 Una sucesión a(n) es acotada inferiormente cuando ninguno de sus términos es menor que algún número K:
Una sucesión a(n) es acotada inferiormente cuando ninguno de sus términos es menor que algún número K:
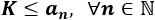 Una sucesión a(n) es acotada cuando es acotada superior e inferiormente:
Una sucesión a(n) es acotada cuando es acotada superior e inferiormente:
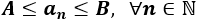
Ejemplos
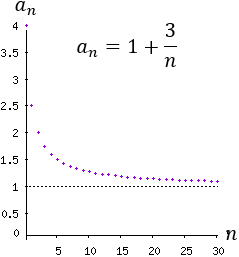
Ejemplo 1: La sucesión a(n) = 1 + 3/n es acotada inferiormente por 1 y superiormente por a(1)=4:
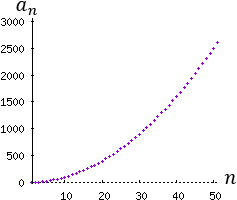
 Ejemplo 2: La sucesión a(n) =n^2 es acotada inferiormente por a(1)=1, pero no es acotada superiormente:
Ejemplo 2: La sucesión a(n) =n^2 es acotada inferiormente por a(1)=1, pero no es acotada superiormente:
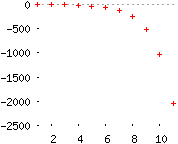
 Ejemplo 3: La sucesión a(n) =-2^n es acotada superiormente por -1/2, pero no es acotada inferiormente:
Ejemplo 3: La sucesión a(n) =-2^n es acotada superiormente por -1/2, pero no es acotada inferiormente:
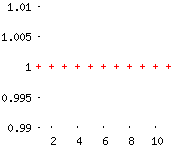
 Ejemplo 4: La sucesión constante a(n) = 1 es acotada:
Ejemplo 4: La sucesión constante a(n) = 1 es acotada:
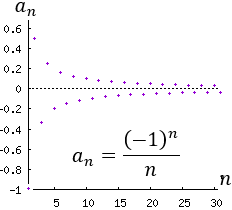
 Ejemplo 5: La sucesión a(n) = (-1)^n/n es acotada (-1≤ a(n) ≤ 1/2):
Ejemplo 5: La sucesión a(n) = (-1)^n/n es acotada (-1≤ a(n) ≤ 1/2):
 Ejemplo 2: La sucesión a(n) =n^2 es acotada inferiormente por a(1)=1, pero no es acotada superiormente:
Ejemplo 2: La sucesión a(n) =n^2 es acotada inferiormente por a(1)=1, pero no es acotada superiormente:
 Ejemplo 3: La sucesión a(n) =-2^n es acotada superiormente por -1/2, pero no es acotada inferiormente:
Ejemplo 3: La sucesión a(n) =-2^n es acotada superiormente por -1/2, pero no es acotada inferiormente:
 Ejemplo 4: La sucesión constante a(n) = 1 es acotada:
Ejemplo 4: La sucesión constante a(n) = 1 es acotada:
 Ejemplo 5: La sucesión a(n) = (-1)^n/n es acotada (-1≤ a(n) ≤ 1/2):
Ejemplo 5: La sucesión a(n) = (-1)^n/n es acotada (-1≤ a(n) ≤ 1/2):

Recursos de progresiones o sucesiones:
- Test básico
- Tipos de sucesiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones aritméticas y geométricas
- Sucesión de Fibonacci
- Calculadoras de progresiones aritméticas
- Calculadoras de progresiones geométricas
- Operaciones entre sucesiones
- Límites de sucesiones
- Subsucesiones
- Introducción a las sucesiones (PyE)
- Criterio de la media aritmética
- Criterios de la media geométrica y de la raíz
- Criterio de Stolz del cociente