Dedução formal
Dedução
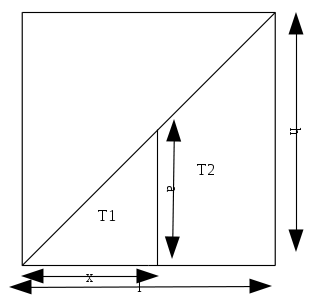
Sejam os triângulos T1 e T2 dados no desenho acima, com a largura de T2 dada por l, constante, a altura de T2 dada por h, constante, o comprimento de T1 dada por x e a altura de T1 dada por a.
Pela semelhança de triângulos, sabemos que , de onde se tira que . Por outro lado, sabemos que a área de T1 é dada por . Substituindo-se o a previamente encontrado, a fim de reescrevermos a relação em termos de x, temos que ,de onde vem que . Como h e l são constantes, concluímos que a área em relação a x é fornecida através de uma função quadrática e, portanto, a mesma descreve uma parábola.
Se, no triângulo T1, em vez de termos isolado a altura a em função de x, tivéssemos isolado o comprimento x em função da altura a, teríamos . .Daí, tiraríamos que , o que também descreve uma função quadrática e, portanto, também descreve uma parábola. No entanto, como l e h, constantes, são na verdade a largura e a altura, respectivamente, de um retângulo e, por construção, esse retângulo é mais largo do que alto (l > h), a curva formada por esta segunda equação estará “antes” da curva da primeira, isto é, a imagem dos pontos x = a por y = A(a) será menor ou igual à dos pontos x = x por y = A(x).