Mehrfache Polstellen und ihr Aussehen
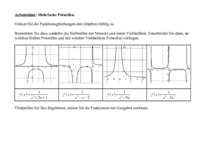
Vergleichen wir die Funktionen und . Unten finden Sie dazu Wertetabellen, in deren linke Hälften noch die richtigen y-Werte eingetragen werden müssen. Erschließen Sie diese y-Werte aus den y-Werten der jeweiligen rechten Seite, ohne zu rechnen.
Immer wenn Sie einen richtigen Wert eintragen, erscheint der entsprechende Punkt im Koordinatensystem, und nach und nach ergeben sich die beiden Funktionsgraphen.
Wir sehen: An den Stelle x = 0 haben beide Funktionen eine Definitionslücke und jeweils eine Polstelle. Diese sehen aber verschieden aus:
hat eine Polstelle erster Ordnung (ersten Grades). Hier wechselt der Graph beim Übergang von links nach rechts das Vorzeichen. Man spricht von Polstelle mit Vorzeichenwechsel (VZW).
hat eine Polstelle zweiter Ordnung (zweiten Grades). Hier wechselt der Graph beim Übergang von links nach rechts das Vorzeichen nicht. Man spricht von Polstelle ohne Vorzeichenwechsel (VZW).
Es gibt auch dreifache oder vierfache Pole usw. Dabei gilt, dass ungerade Pole wie einfache Pole aussehen und gerade Pole wie zweifache Pole aussehen.
Als Ergebnis halten wir fest:

Wir wissen bereits: Polstellen liegen bei den x-Werten vor, bei denen der Nenner null, d.h. bei denen durch Null geteilt wird.
Beispiele: hat einen einfachen Pol mit VZW an der Stelle x = 3.
hat einen zweifachen Pol ohne VZW an der Stelle x = -4.
hat eine siebenfache Pol mit VZW an der Stelle x = 6.
Natürlich kann eine gebrochen-rationale Funktion auch verschiedene Polstellen gleichzeitig aufweisen.
Beispiel: hat einen einfachen Pol mit VZW an der Stelle x = -1 und einen zweifachen Pol ohne VZW an der Stelle x = 2. Der Graph hat also zwei senkrechte Asymptoten (und für eine waagerechte Asymptote). Dies zeigt sich am Graphen:

Beachten Sie auch:
Eine gebrochen-rationale Funktion hat einen ein-, zwei-, dreifachen usw. Pol an der Stelle, an der ihr Nenner eine ein-, zwei-, dreifache usw. Nullstelle hat. Machen Sie sich dies auch am letzten Beispiel klar.
Sie können nun anhand des folgenden Arbeitsblattes prüfen, ob Sie dieses Kapitel verstanden haben.