Outline
Feynmanův trojúhelník
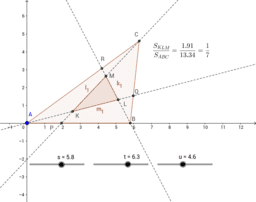
Feynmanův trojúhelník - máme-li libovolný trojúhelník ABC v rovině. Vždy v jedné třetině každé jeho strany umístíme postupně body P, Q, R a spojíme je s protilehlými vrcholy. Průsečíky těchto spojnic jsou vrcholy trojúhelníku KLM, potom tento trojúhelník má obsah o velikosti jedné sedminy obsahu trojúhelníku ABC.
Feynmanův trojúhelník je zobecněním Routhovy věty (dostupné na: https://www.geogebra.org/m/vmP2axQA), tímto vztahem mezi obsahy trojúhelníků se zabýval americký fyzik Richard Feynman, držitel Nobelovy ceny za fyziku. S výše uvedeným tvrzením se seznámil na společenském večírku, kde se celý večer snažil vyvrátit toto tvrzení. Výsledkem jeho snažení bylo, že dané tvrzení dokázal pomocí kosinové věty a vět o podobnosti pro rovnostranný trojúhelník. Odtud následně svůj důkaz zobecnil pro obecný trojúhelník na základě myšlenky, že afinní obraz obecného trojúhelníku je trojúhelník rovnostranný.
Zdroje:
[1] De VILLIERS, M.: Feynman's Triangle: Some Feedback and More. [online]. [cit. 2017-02-07].
Dostupné z: http://mysite.mweb.co.za/residents/profmd/feynman.pdf
[2] One seventh area triangle. In: Wikipedia: the free encyclopedia [online]. San Francisco (CA): Wikimedia Foundation, 2001- [cit. 2017-02-07].
Dostupné z: http://en.wikipedia.org/wiki/One-seventh_area_triangle
[3] ŠTRAUSOVÁ, I.: Speciální případ Routhovy věty a jeho důkaz v geogebře [online]. [cit. 2017-02-07].
Dostupné z: http://home.pf.jcu.cz/~sbml/wp-content/uploads/Strausova1.pdf