Composizione di due simmetrie assiali con assi perpendicolari (Classe II-III)
Disegna il primo asse di simmetria con lo strumento Retta
,disegna il secondo asse di simmetria, perpendicolare al primo e passante per A o B, con lo strumento Retta perpendicolare
,con lo strumento Angolo
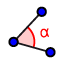metti in evidenza l’angolo retto formato dai due assi di simmetria,disegna un triangolo con lo strumento Poligono
,con lo strumento Simmetria assiale
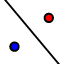fai la composizione delle due simmetrie assiali.
Rispondi alle domande
Osserva il triangolo iniziale e il suo simmetrico. Secondo te, sono congruenti? Motiva la tua risposta anche con l’aiuto degli strumenti di GeoGebra.
Secondo te, esiste un’isomeria che manda direttamente C in C′′, D in D′′ e E in E′′? Se si quale?
Per rispondere alla domanda o per verificare la tua ipotesi gli strumenti di GeoGebra che possono aiutarti sono: lo strumento Segmento lo strumento Punto medio o centro 
per congiungere un vertice della figura iniziale con il suo corrispondente nella figura finale,
per individuare i punti medi dei segmenti che congiungono vertici corrispondenti.
Le proprietà che hai scoperto restano valide anche se muovi i punti con lo strumento Muovi 
? E se muovi gli assi di simmetria?
Prova quindi a completare la definizione dell’isometria studiata (composizione di due simmetrie assiali con assi di simmetria perpendicolari tra loro):
“Ad ogni punto P del piano questa isometria associa un punto P’ tale che...
Quale strumento di GeoGebra potresti utilizzare per avere un’ulteriore conferma che la composizione di due simmetrie assiali con assi perpendicolari è una particolare isometria?
Quali rette “notevoli” del piano cartesiano si possono utilizzare per effettuare una composizione di simmetrie assiali con assi perpendicolari?
nella vista Grafici lasciare sia la griglia che gli assi cartesiani,
con lo strumento Punto
individua i seguenti punti nel piano cartesiano: A(3,2), B(5,0), C(0,1) e D(−1,4) e scegli nella barra degli stili Nome e Valore in modo che le coordinate siano visibili nella vista Grafici,con lo strumento Simmetria assiale
trova i simmetrici A′, B′, C′ e D′ dei punti dati rispetto all'asse delle ordinate.
Rispondi alla domanda Osserva le coordinate dei simmetrici. Secondo te, esiste una relazione che lega le coordinate di uno dei punti dati e del suo simmetrico rispetto all'asse y?
- Dalla vista Algebra nascondi i punti A, B, C e D,
- con lo strumento Simmetria assiale trova i simmetrici A′′, B′′, C′′ e D′′ dei punti A′, B′, C′ e D′ rispetto all'asse delle ascisse.
Rispondi alla domanda Osserva le coordinate dei punti simmetrici. Secondo te, esiste una relazione che lega le coordinate di uno dei punti dati e del suo simmetrico rispetto all'asse x?
Segui il seguente passo
Dalla vista Algebra mostra solo i punti A, B, C, D, A′′, B′′, C′′, D′′
Rispondi alle domande
Osserva le coordinate di A e di A′′. Secondo te, esiste una relazione che lega le coordinate di uno dei punti e del trasformato rispetto alla composizione delle due simmetrie?
Quale isometria manda direttamente il punto A in A′′, B in B′′, C in C′′ e D in D′′? Verifica la risposta anche con lo strumento di GeoGebra opportuno.