Die Exponentialfunktion
Definition
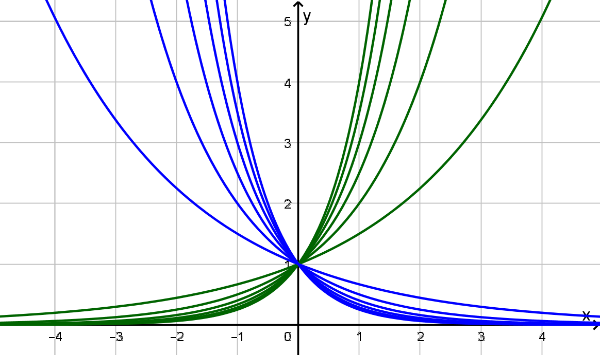
Eine Exponentialfunktion ist definiert als Funktion, deren Funktionsgleichung in der Form
geschrieben werden kann.
Dabei ist die stets positive Basis q der so genannte Wachstumsfaktor. Er gibt an, mit welchem Faktor der Funktionswert multipliziert wird, wenn x um 1 erhöht wird.
Funktionsgleichung von Exponentialfunktionen
Aufgabe: Charakteristika von Exponentialfunktionen graphisch untersuchen
Verändern Sie im Diagramm
und notieren Sie, was Sie dabei feststellen.
Anfangswert
Die Funktion f mit ; kann modifiziert werden, sodass ihr Graph statt des y-Achsenabschnitts 1 jeden beliebigen y-Achsenabschnitt annehmen kann. Dazu wird der Graph um einen Parameter a in y-Richtung, d.h. vertikal gestreckt. Die Funktionsgleichung der modifizierten Funktion g lautet:
Hierbei ist a der sogenannte Anfangswert des exponentiellen Wachstums/Zerfalls.
Aufgabe: Anfangswert und Wachstumsfaktor graphisch bestimmen
Stellen Sie q und a im nächsten Diagramm so ein, dass gilt: und notieren Sie a und q.
Aufgabe: Zuordnung von Funktionsgleichungen und Schaubildern
Aufgabe: Funktionsbestimmung mit einem Punkt
Schauen Sie sich das folgende Video von Daniel Jung (https://youtu.be/ZTBkpiCWIMg) aufmerksam an und lösen Sie anschließend folgende Aufgabe: Bestimmen Sie q, sodass der Graph der Funktion f mit f(x)=qx durch den Punkt P(2|8) verläuft.
Aufgabe: Funktionsbestimmung mit zwei Punkten
Schauen Sie sich das zweite Video von Daniel Jung (https://youtu.be/bsI4GjTioGQ) an und lösen Sie folgende Aufgabe: Bestimmen Sie a und q, sodass der Graph der Funktion g mit g(x)=aqx durch die Punkte Q(0|-4) und R(2|-1) verläuft.