Teorema de Pitágoras
Demostraciones del Teorema de Pitágoras hay muchas, la que mostramos está basada en la potencia de un punto. Recordamos:
Dado un punto P en el plano y una circunferencia c. Si trazamos una recta que pase por P y corte a la circunferencia en dos puntos A y B, entonces, el producto de la distancias PA y PB es constante. A esta constante se llama potencia de un punto P.Obviamente el punto P puede se interior o exterior a la circunferencia. Ahora sí, construyamos nuestra demostración del Teorema de Pitágoras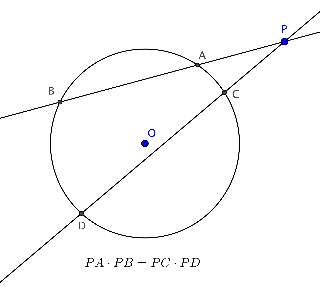
Observemos primero que CD+DB=a. Dado que A es un ángulo recto el segmento AC es tangente a la circunferencia que pasa por A, D y B. Por tanto, usando que la potencia de C es constante, obtenemos:
o
Repetimos el argumento con el punto B y la circunferencia que pasa por A, D y C y obtenemos que: o
Sumando ambas expresiones obtenemos:
Obteniendo:
Como hemos visto, una demostración sin palabras no quiere decir una demostración sin pensar.
Construcción
- Con el botón
dibujamos dos puntos A y B. - Escribimos en la barra de entrada: recta[A,B] o usamos el botón
para trazar la recta que pasa por A y B. - Con el botón
trazamos la recta perpendicular que pasa por A. - Situamos un punto en la recta perpendicular, el punto C.
- Ocultamos las dos rectas anteriores haciendo clic en
de la recta en la vista algebraica. - Con el botón
dibujamos el triángulo rectángulo de vértices, A, B y C. - Trazamos la altura por el vértice A usando el botón y marcamos su intersección
con el lado del triángulo. A continuación, ocultamos la recta. - Dibujamos el segmento AD escribiendo en la barra de entrada: Segmento[A,D] o usando el botón
. - Trazamos con el botón las circunferencias que pasan por A,D y C y A,D y B.