Un esempio concreto: le componenti dei vettori
Prima ancora di conoscere le complesse regole della goniometria e delle trigonometria, vediamo a cosa potrà servirci saper lavorare con gli angoli e le loro proprietà. Per fare questo dobbiamo ripassare un concetto che con ogni probabilità hai già incontrato in Fisica: le grandezze vettoriali.
Ricordiamo che mentre una grandezza si dice "scalare" se è completamente definita da un valore numerico (ad esempio un'età, un prezzo o la massa di un oggetto), le grandezze vettoriali descrivono fenomeni più complessi, e quindi hanno bisogno di più informazioni per essere definite. Vediamo questo concetto nella breve animazione qui sotto.
Una tecnica molto importante che si utilizza lavorando con le grandezze vettoriali è la scomposizione in componenti. Infatti è molto utile saper vedere una grandezza vettoriale come somma di vettori orientati in certe direzioni: scegliendo in modo opportuno queste direzioni, si può infatti descrivere la grandezza vettoriale come combinazione di fenomeni più facili da interpretare e calcolare.
Questa operazione, che è strettamente legata alla somma di vettori, è descritta nell'animazione seguente.
L'ultimo esempio mostrato nell'animazione ci permette di intuire la relazione che tutto questo ha con gli angoli e con la goniometria: poiché un vettore e le sue componenti sono inclinati l'uno rispetto alle altre di un certo angolo, se vogliamo sapere la lunghezza di questi vettori (cioè il loro modulo) abbiamo bisogno di conoscere come si lavora con gli angoli.
Vediamo il concetto in termini più generali qui sotto.
Vediamo ora un primo esempio in cui, dato un vettore di conosciamo il modulo (cioè la lunghezza), riusciamo a calcolare il modulo (cioè la lunghezza) di una delle sue componenti. Potremo svolgere questo calcolo perché inclineremo il vettore di un angolo molto particolare, che ha proprietà che ci aiuteranno.
DAL RISULTATO PARTICOLARE AL CONCETTO GENERALE
Riportiamo qui sotto la figura che abbiamo utilizzato, per poter ragionare sul risultato ottenuto.
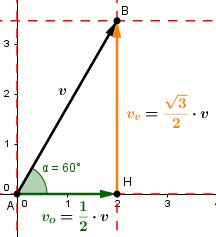
La figura mostra come, grazie ai nostri calcoli, siamo riusciti ad ottenere la misura delle due componenti rispetto a quella del vettore originale: per un vettore inclinato di 60° rispetto all'orizzontale abbiamo ottenuto che
- la componente orizzontale è pari a metà - cioè - del vettore originale
- la componente verticale è pari a del vettore originale
- In teoria potremmo scomporre un vettore lungo direzioni qualsiasi ma di fatto vedremo che lavoreremo sempre con direzioni perpendicolari tra loro, quindi le due componenti di fatto saranno, in termini puramente geometrici, i due cateti di un triangolo rettangolo, di cui il vettore originale è l'ipotenusa.
- Il caso di componente "orizzontale" e verticale" è un esempio specifico: in generale le direzioni lungo le quali scomporre il vettore possono essere qualsiasi, in generale non si parla di componente "orizzontale" o "verticale" ma del cateto "adiacente all'angolo", cioè che lo tocca (nel nostro esempio quello verde), e quello opposto all'angolo (nel nostro esempio l'arancione). Vedi anche l'esempio riportato sotto.
![Il piano inclinato è un altro esempio in cui, data [b]la forza peso [math]\large{P}[/math] dell'oggetto[/b], è utile capire quanto misura la [b][color=#38761d]componente parallela al piano[/color][/b], che fa scivolare l'oggetto lungo il piano, e [color=#ff0000][b]quella perpendicolare[/b][/color], che ostacola il moto a causa dell'attrito tra l'oggetto stesso ed il piano.
Le due componenti non sono né orizzontale né verticale, ma come nel primo esempio esse [b][color=#980000]formano un triangolo rettangolo di cui la forza peso è l'ipotenusa[/color][/b], [color=#38761d][b]una componente è il cateto opposto all'angolo [math]\large{\alpha}[/math] [/b][/color]e [color=#ff0000][b]l'altra è quello adiacente ad esso[/b][/color]. La geometria del problema è quindi identica.](https://www.geogebra.org/resource/phk6tsa5/Tew8vEIffCExW8nj/material-phk6tsa5.png)
Diamo ora due prime definizioni GENERALI delle grandezze goniometriche che stiamo conoscendo.
Il rapporto tra il cateto (componente, nei nostri esempi) adiacente all'angolo e l'ipotenusa (il vettore originale dei nostri esempi) viene chiamato coseno dell'angolo.
Considerando il nostro primo esempio e partendo dalla relazione , possiamo dire anche che .
Il rapporto tra il cateto opposto all'angolo e l'ipotenusa Il coefficiente "arancione" è chiamato seno dell'angolo.
Sempre riconsiderando il primo esempio abbiamo:
.
Abbiamo fatto quindi la nostra prima scoperta di goniometria: e .
I due numeri che abbiamo ottenuto si riferiscono all'angolo particolare di 60°; rivediamo quindi innanzitutto la definizione generale di seno e coseno in questa breve animazione.
Stiamo scoprendo che un qualsiasi angolo , possiamo definire il seno ed il coseno di costruendo sui suoi lati un triangolo rettangolo, cioè scomponendo uno dei due lati nella direzione dell'altro lato ed in quella perpendicolare ad esso.
Definiamo il seno dell'angolo il rapporto tra il cateto opposto all'angolo (quella che nell'esempio iniziale era la componente "verticale") e l'ipotenusa (il vettore inclinato dell'angolo ), mentre il coseno dell'angolo è il rapporto tra il cateto adiacente all'angolo (quella che nell'esempio iniziale era la componente "verticale") e l'ipotenusa.
Una osservazione molto importante è che i due cateti sono sempre minori dell'ipotenusa (nel nostro esempio, le componenti del vettore sono sempre minori... o uguali al vettore originale), quindi seno coseno di un angolo sono sempre due numeri inferiori o uguali a 1.
È evidente che se avessimo considerato un angolo molto piccolo la componente orizzontale sarebbe stata quasi uguale al vettore originale (e quindi avremmo ottenuto un coseno di poco inferiore ad uno), mentre la componente verticale sarebbe stata una frazione minima del vettore (e quindi il seno sarebbe stato un numero molto piccolo e vicino allo zero). Puoi visualizzare quanto detto nell'immagine sotto.
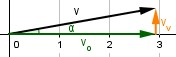
Al contrario per un angolo di poco inferiore a 90° avremo un coseno molto piccolo ed una componente verticale quasi identica al vettore originale (e quindi un seno di poco inferiore ad 1).
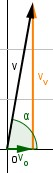
Allo stesso modo puoi ipotizzare come saranno il seno ed il coseno degli altri angoli, in particolare di quelli mostrati nell'animazione "GLI ANGOLI E LE COMPONENTI DI UN VETTORE" vista prima.
UNA TERZA DEFINIZIONE... ED UN VECCHIO CONOSCENTE
Esiste una terza grandezza goniometrica fondamentale, che è in relazione con le prime due ma ha un suo significato ed una sua utilità distinte.
Definiamo tangente di un angolo il rapporto tra la componente opposta all'angolo (cateto opposto) e quella adiacente (cateto adiacente).
| Seguendo questo ragionamento, puoi ipotizzare quanto vale il seno di 90°? Ed il suo coseno? Cerca di dedurre quanto valgono seno e coseno di 0°. |
| Secondo te per quale angolo otterremo che i due coefficienti sono uguali? |
![Utilizzando la stessa costruzione introdotta per il seno ed il coseno, definiamo [color=#ff0000][b]la tangente di un angolo[/b][/color] come il rapporto tra il [b][color=#ff7700]cateto opposto[/color][/b][color=#ff7700][b] all'angolo[/b][/color] ed il [b][color=#274e13]cateto adiacente all'angolo[/color][/b].](https://www.geogebra.org/resource/z5dtbmsq/Yyfth7qA8vEO0aCx/material-z5dtbmsq.png)
Se riproponiamo la stessa immagine in un formato leggermente diverso, vediamo che nell'ambito della geometria analitica la tangente coincide con un'importante caratteristica della retta.
![Visualizzando geometricamente la definizione di coefficiente angolare ci accorgiamo che questo valore coincide con [color=#ff0000][b]la tangente dell'angolo che la retta forma con l'asse delle [/b][math]\large{x}[/math][/color] (più esattamente con il semiasse positivo). Quindi l'angolo [math]\alpha[/math] in questo caso sarà quell'angolo che ha tangente uguale a 2 - impareremo ad ottenere questo valore grazie alla calcolatrice.](https://www.geogebra.org/resource/cwuvg9xp/hTehQDxnUAT6EsWg/material-cwuvg9xp.png)