Notion de valeur moyenne de fonction - intégrale
Voici une définition possible de valeur moyenne d'une fonction continue sur un intervalle [a;b]
On considère une fonction f, continue sur l'intervalle [a;b].
La valeur moyenne de f sur l'intervalle [a;b] est le nombre tel que l'aire du rectangle ABCD et l'aire située sous la courbe de la fonction f soient égales.
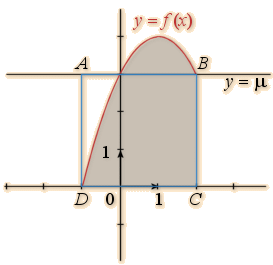 Graphiquement, s’interprète comme la longueur AD ou BC du rectangle.
Graphiquement, s’interprète comme la longueur AD ou BC du rectangle.
 Graphiquement, s’interprète comme la longueur AD ou BC du rectangle.
Graphiquement, s’interprète comme la longueur AD ou BC du rectangle.
Pour illustrer et manipuler
Exercice : A l'aide de la feuille dynamique au-dessus et en manipulant les curseurs à disposition, déterminer une valeur, exacte ou approchée au centième, de la valeur moyenne de chacune des fonctions suivantes, sur l'intervalle indiqué :
1) valeur moyenne de la fonction f sur l'intervalle [1;8]
2) valeur moyenne de la fonction f sur l'intervalle [2;7]
3) valeur moyenne de la fonction g sur l'intervalle [2;8]
4) valeur moyenne de la fonction h sur l'intervalle [-1;6] 5) valeur moyenne de la fonction sur l'intervalle [2;7] 6) valeur moyenne de la fonction sur l'intervalle [2;7] 7) valeur moyenne de la fonction sur l'intervalle [2;7]