3 typer symmetri i mønstre
Spejling, parallelforskydning og drejning i mønstre
Når vi taler om symmetri i hverdagen, handler det tit om, at vi synes, noget er "pænt" og harmonisk. Vi mener også for det meste spejling, når vi taler om symmetri.
I matematik kan symmetri også komme, ved at man laver parallelforskydninger (skubninger) og drejninger (rotationer) af figurer.
Hvis figurerne i et mønster er gentaget og ikke ændrer form, er der symmetri. Figurerne kan dog godt ændre placering og den retning, de vender.
Herunder er der billeder af mønstre, hvor de tre typer flytning er brugt til at lave symmetri.
Symmetri med spejling
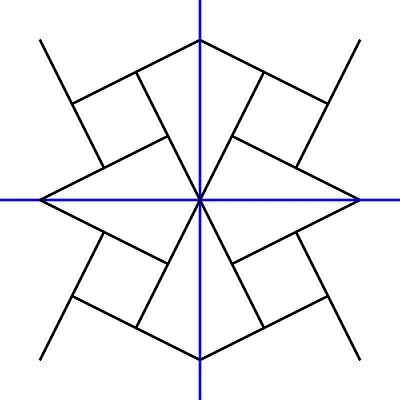

Symmetri med parallelforskydning


Symmetri med drejning
