Ficha 6: Funciones y ecuaciones
En este capítulo estudiaremos uno de los puntos fuertes de Geogebra, que es el trabajo con funciones y ecuaciones. Para ello haremos uso de la Barra de entrada que se encuentra en la parte inferior. Si introducimos la expresión en la barra de entrada (tal cual aparece aquí), el programa respetará la notación funcional (nota: también es posible introducir solamente la expresión ). En cambio si anotamos la expresión el programa lo interpretará como una ecuación y le asignará un nombre a la recta que representa. Geogebra se encargará de nombrar las funciones y ecuaciones en orden y sin repetir, y en el caso de reescribir, por ejemplo f(x) se interpretará como una re-definición de la función anterior, por lo que se reemplazará la recta anterior por la nueva expresión.
Como se ha visto en la introducción de este capítulo, representar una función es tarea sencilla, solo necesitamos ingresar la expresión matemática de la función en la barra de herramientas y aceptar presionando la tecla "enter" o "intro". Por ejemplo, para representar la función hacemos clic en la barra de entrada, luego anotamos "f(x)=3/2x+2" y damos "enter". Aparecerá la recta en nuestra pantalla. Esta misma recta puede ser introducida como una ecuación: "y=3/2x+2". En este caso el programa asociará la primera letra del abecedario disponible en el dibujo para nombrarla. Obviamente la gráfica será la misma.
Este apartado es similar al anterior con la única diferencia que para introducir términos cuadráticos (y exponentes en general) GeoGebra tiene un asistente a la izquierda de la barra de entrada, con forma de teclado, que contiene constantes, símbolos, operaciones y funciones matemáticas elementales. Para introducir exponentes el teclado del ordenador posee la tecla del acento circunflejo (^) que se utiliza de igual forma en las calculadores científicas. Por ejemplo la función de la gráfica siguiente se puede introducir de la siguiente manera: f(x)=-2x^2+3 (en general hay que presionar la combinación "shift" + "^" y luego la barra espaciadora para que aparezca en pantalla este acento).
La función bicuadrada es un caso particular de función polinómica. Su introducción en la barra de entrada responde a la misma sintaxis. Por ejemplo: f(x)=x^4-4x^2. El resto de funciones polinómicas se introducen de igual manera.
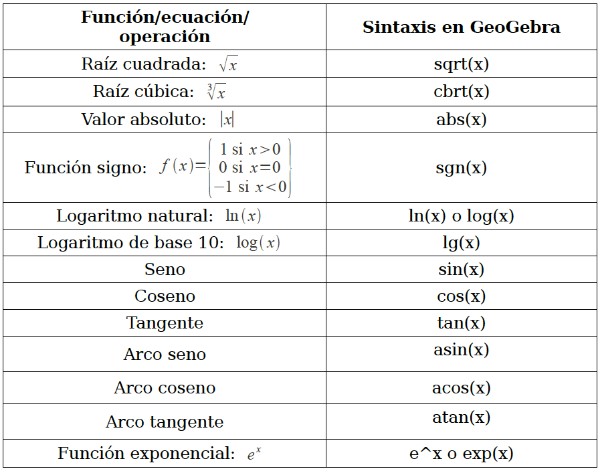
Para introducir algunas funciones especiales utilizaremos el asistente ubicado a la izquierda de la barra de entrada o en su defecto podremos escribirlas directamente con el teclado según la siguiente tabla. Nota: recordemos que el programa utiliza el idioma inglés como base para las expresiones matemáticas.