Sinus&cosinus
Introduction à la trigonométrie
Sinus et cosinus
En rouge, deux points sont liés au centre du repère cartésien Les pointillés noirs qui lient les points bleus et rouges restent parallèles aux axes x et y Alors que le point bleu se déplace le autour du cercle, ces deux points rouges se déplacent sur les axes x et y La coordonnée x du point se déplaçant sur l'axe y est le sinus de l'angle en vert La coordonnée y du point se déplaçant sur l'axe x est le cosinus de l'angle en vert On notera ces nombres sin(AOE) et cos(AOE), leur valeur est comprise entre -1 et 1 Sachant qu'on mesure les angles dans le sens dit "trigonométrique", c'est-à-dire le sens anti-horloger (convention), comment désigne-t-on l'angle en vert du schéma simplifié suivant ?
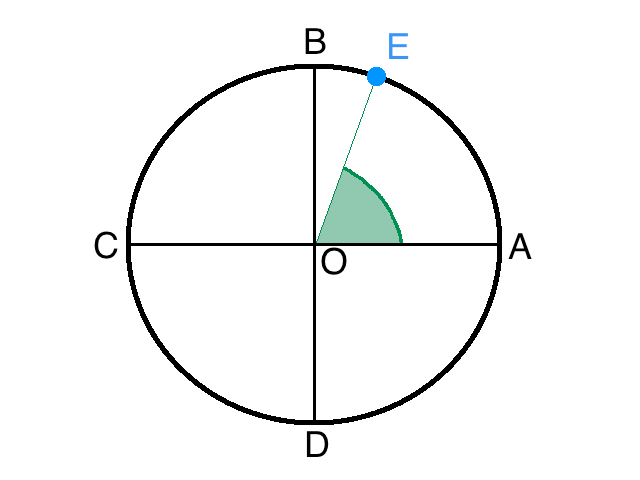
Question 1
Coche ci-dessous la meilleure approximation de sin(120°) ? Déplace le point bleu pour répondre à la question (clique et fais glisser autour du cercle)
Question 2
Coche ci-dessous la meilleure approximation de sin(20°) ? Déplace le point bleu pour répondre à la question (clique et fais glisser autour du cercle)
Question 3
Coche ci-dessous la meilleure approximation de cs(40°) ? Déplace le point bleu pour répondre à la question (clique et fais glisser autour du cercle)
Question 4
Coche ci-dessous la meilleure approximation de cos(240°) ? Déplace le point bleu pour répondre à la question (clique et fais glisser autour du cercle)
Question 5
Réarrange la relation suivante pour qu'elle soit vraie : sin(40°)‹sin(50°)‹cos(40°)‹cos(50°)‹sin(10°)‹sin(170°)‹cos(10°)‹cos(170°)