Математичний маятник
Міжпредметні завдання
2. Нитку математичного маятника відхилили до горизонтального положення і відпустили. Яка мінімальна міцність нитки F, якщо маса маятника m?
3. Графік якої функції описують коливальні рухи маятника? Запишіть формулу.
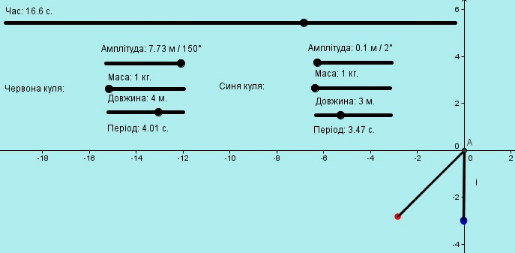
4. Знайдіть координати точок центрів червоної та синьої кулі, у випадках коли вектор натягу нитки знаходиться під кутом : 1) 30; 2) 45; 3) 90; 4) 120 градусів до осі ОХ. При цьому показники повзунків мають такі значення: амплітуда в двох випадках-максимальна; маса червоної кулі 2 кг, синьої 5 кг; довжина 5 м та 2.5 м відповідно.
5. Домалюйте одну зі сторін трикутника утвореного натягами ниток(див. малюнок) та обчисліть його периметр та площу.
6. Згадайте, де в повсякденному житті, в природі ви зустрічаєтесь з подібними явищами? Опишіть дані явища.
