Геометрические тела
| Геометрическое тело — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы. Геометрическое тело возможно выделить замкнутой поверхностью, т.е. его границей. Еще геометрическим телом можно назвать компактное множество точек, и 2 точки из множества возможно соединить отрезком, этот отрезок целиком проходит внутри границы тела, это указывает на то, что геометрическое тело состоит из множества внутренних точек. Наружная граница геометрического тела является его гранью, у тела может быть одна либо несколько граней. Множество плоских граней определяет множество вершин и ребер геометрического тела. Все геометрические тела делятся на многогранники и тела вращения. Тела вращения. Тела вращения — это объёмные тела, которые возникают следствием вращения плоской геометрической фигуры, которая ограничена кривой, вокруг оси. Эта ось лежит в той же плоскости. Если вращать контуры фигур, образуется поверхность вращения (к примеру, сфера, которая образовывается из окружности), а если вращать заполненные контуры – возникают тела (шар, который образован из круга). |
| Шар — образуется из полукруга, вращением вокруг диаметра разреза. | 
|
| Цилиндр — образуется из прямоугольника, вращая его вокруг одной из сторон. Площадью боковой поверхности цилиндра берут площадь его развертки: Sбок = 2πrh. |   |
| Конус — образуется из прямоугольного треугольника, при вращении его вокруг одного из катетов. Площадью боковой поверхности конуса берут площадь ее развертки: Sбок = πrl, Площадь полной поверхности конуса: Sкон = πr(l+ r) |   |
| Тор (тороид) — образуется из окружности, вращая ее вокруг прямой, которая не пересекает его. |   |
| Многогранники. Многогранник или полиэдр — зачастую замкнутая поверхность, состоящая из многоугольников. Ее, бывает, зовут тело, которое ограничено этой поверхностью. Многогранник – тело, у которого граница, это объединение ограниченного количества многоугольников. Есть 5 видов правильных многогранников: |
| Тетраэдр |   |
| Гексаэдр (куб) |   |
| Октаэдр |  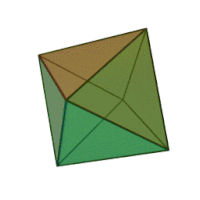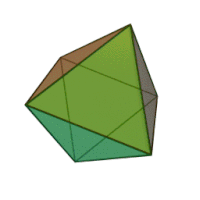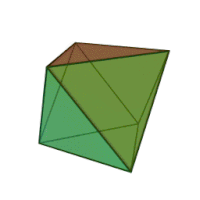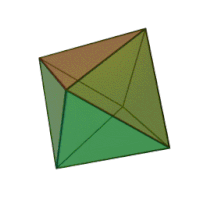 |
| Додекаэдр |  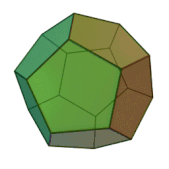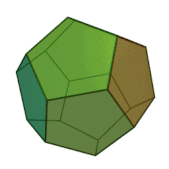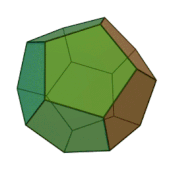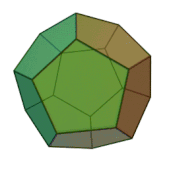 |
| Икосаэдр |  
|
| Правильным многогранником является многогранник, с гранями из правильных равных многоугольников, также, каждый двугранный угол имеет одинаковое значение. Однако существуют другие многогранники – все многогранные углы равны, а грани – правильные, при этом разноименные правильные многоугольники. Такие многогранники являются равноугольно-полуправильными многогранниками. Это: усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр, усеченный икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр, "плосконосый" (курносый) куб, "плосконосый" (курносый) додекаэдр. Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, возможно получить правильные звездчатые многогранники. Таких многогранников существует только 4, еще их зовут телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, и назвал его «колючий» либо «еж», и большой додекаэдр. Пуансо открыл другие 2 правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр. |