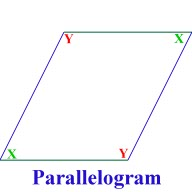
FINDING A FORMULA FOR THE AREA OF A PARALLELOGRAM
Instructions
Introduction and Background
In order to make the task of finding the area of a polygon more efficient, geometers over the years have developed formulas that can be memorized and then applied to problem solving situations. The formulas take what is known about the shape, for example, the length of its sides, and uses that information to find the area. In this activity,you will explore the parallelogram, make observations, and, just like geometers before you, develop a formula which can always be used to find the area of a parallelogram. Step 1. Build a Parallelogram When you open the GeoGebra file, you see three simple polygons: a red rectangle, a blue triangle, and a green triangle. Challenge: Use the MOVE tool to use these three polygons to construct a parallelogram that is not a square or rectangle (see the diagram below). Turn on the GRID and use the grid to measure the length of the base of the parallelogram and the height of the parallelogram: Base = _______________units of length Height= _______________units of length Step 2. Build a Rectangle Challenge: Use the MOVE tool
to change the parallelogram into a rectangle by moving only one triangle.
Turn on the GRID and use the grid to measure the length of the base of the new rectangle and the height of the new rectangle:
Base= _______________ units of length
Height = _______________units of length
You can either count the unit squares in the new rectangle or use the formula for area of a rectangle
area of rectangle = base X height
to find the area of the new rectangle.
The area of the new rectangle made from the parallelogram = ___________ square units.
Then what must be the area of the parallelogram? ___________ square units.
Why do you think so?
Conclusion So, the formula for the area of any parallelogram appears to be the same formula as the area of a rectangle: area = base X height
Test this conclusion. Use the POLYGON tool 
to construct several different parallelograms on this GeoGebra page. Use the grid to measure the base and height of your parallelograms. Then use the grid or the AREA tool 
to find the area of each. Does the formula seem to work for all of your parallelograms?
