Producto de vectores
Producto de un vector por matriz
El producto de un vector por matriz se refiere a la multiplicacion de un vector X con m componentes por una matriz A m x n dando como resultado otro vector.
Representacion
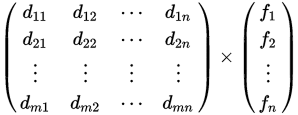
Recuerda: Cuando multiplicamos una matriz por un vector, es necesario que el número de filas del vector coincida con el número de columnas de la matriz. Si no es así, la multiplicación no está definida..
Procedimientos
1. Se multiplican las columnas de la matriz con los renglones correspondientes del vector.
2. Sumamos de manera horizontal.


Multiplicación de un vector por un escalar.
El producto de un escalar por un vector o producto de un vector por un escalar da por resultado otro vector, con la misma dirección que el primero. Al hacer la multiplicación, el escalar cambia el módulo del vector (gráficamente el largo) y en caso de ser negativo cambia también el sentido. La dirección del vector resultado es siempre la misma que la del vector original. Si el escalar es positivo tendrá el mismo sentido y si es negativo tendrán sentido diferentes. Matemáticamente esto se realiza multiplicando al escalar por cada una de las componentes del vector. Si por ejemplo el vector V tiene 2 coordenadas: V = (x, y) k V = k (x, y) = (kx, ky) Ejemplo: V = (2,1) k = 2 k V = 2 (2, 1) = (4, 2) V= (2, 2) k = -1 k V = -1 (2, 2) = (-2, -2)Producto escalar de dos vectores
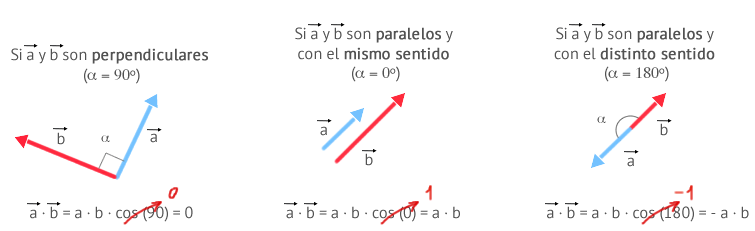
Producto escalar de dos vectores es un numero real que resulta al multiplicar el producto de sus módulos por el coseno del angulo que forman. El producto escalar de un vector a y otro b, denotado como a ⋅ b devuelve un número (escalar) tal que, a ⋅ b= ∣a∣ ⋅ ∣b∣ ⋅ cos(α) El cálculo del producto escalar de estos dos vectores se simplifica cuando estos son perpendiculares o paralelos entre si:- Si son perpediculares, el ángulo forma 90º y el producto es 0
- Si son paralelos, tenemos dos posibilidades:
- Si tienen el mismo sentido, el producto escalar es la multiplicación de sus módulos
- Si NO tiene el mismo sentido, el producto escalar es la multiplicación de sus módulos añadiéndole el signo negativo.