Hoch- Tief- und Sattelpunkt rechnerisch
Im vorigen Kapitel haben wir die folgende Strategie anschaulich erarbeitet:
- Suche nach Stellen mit waagrechter Tangente
- Für jeden Kandidaten anhand der Steigung in seiner Umgebung entscheiden, ob es ein Hoch-, ein Tief- oder ein Sattelpunkt ist.
1. Stellen mit waagrechter Tangente
Für Stellen x mit waagerechter Tangente gilt, dass dort die Ableitung der Funktion Null ist, denn Ableitung bedeutet ja Steigung der Tangenten an dieser Stelle. Das heißt, dass wir diese Stellen finden, indem wir die Ableitung Null setzen: . Wenn wir diese Gleichung nach x auflösen, bekommen wir alle Kandidaten für Hoch-, Tief und Sattelpunkte.
Beispiel:
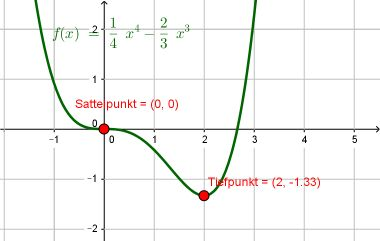
Wir untersuchen die folgende Funktion auf Extrempunkte: .
Die Ableitung lautet .
Ansatz:
Ausklammern von liefert: .
Diese Gleichung hat die beiden Lösungen und . An diesen beiden Stellen gibt es also eine waagrechte Tangente. Das sind also die Kandidaten für Extremstellen.
2. Hochpunkt, Tiefpunkt oder Sattelpunkt?
Wir wollten (vgl. letztes Kapitel) bei jedem Kandidaten schauen, wie sich die Steigung beim Überschreiten ändert:
- bergauf bergab: Hochpunkt
- bergab bergauf: Tiefpunkt
- vorher und nachher gleich: Sattelpunkt