Variable estadística bidimensional

Autor:Projecte La Salle Bonanova - Sant Gabriel Viladecans, Manel Martínez i Pascual

Una variable estadística bidimensional resulta quan estudiem dues característiques diferents dels individus d'una població. Per exemple: Estudiem el pes (X) i l'alçada (Y) dels alumnes d'una classe. La variable bidimensional és (X,Y). X i Y són variables estadístiques unidimensionals.

Taules de doble entrada

A 20 alumnes de batxillerat se'ls va demanar la qualificació final de matemàtiques (X) i física (Y). Els resultats van ser els següents: (X,Y)={(4,3), (5,6), (6,7), (7,7), (7,8), (8,8), (7,6), (8,7), (7,5), (2,3), (4,5), (6,4), (6,5), (5,3), (3,4), (4,5), (5,4), (6,5), (9,7), (3,3)} Per organitzar les dades emprarem una taula de doble entrada, on introduirem els diferents valors observats per cadascuna de les dues variables unidimensionals, i les freqüències absolutes en cada cas.

Activitat 12

Respon les següents preguntes, tot explicant com obtens els resultats:

Quants alumnes va obtenir com a mínim un 7 de matemàtiques?
Quants alumnes van treure una nota superior a 5 en física?
Quin tant per cent dels alumnes van treure una nota superior a física que en matemàtiques?
Quin tant per cent del alumnes tenen la mateixa nota de física que de matemàtiques?

Taules de freqüències marginals i covariància

Les taules de freqüències marginals són les que s'obtenen d'estudiar cadascuna de les variables unidimensionals per separat. La covariància d'una variable bidimensional,

, és una mesura de dispersió conjunta.

$\sigma_{XY}=\frac{1}{n} \sum_{i=1}^{n} \left(x_i - \bar{x} \right) \cdot \left(y_i - \bar{y} \right)= \frac 1 n\sum_{i=1}^{p}\sum_{j=1}^{q} n_{ij}\ x_i\cdot y_j-\bar{x}\bar{y}$

En el cas de l'exemple anterior, $\bar{x}=5.6\text{ i }\bar{y}=5.3$ $\sigma_{XY}=\frac{1}{20}\left(1\cdot2\cdot3+1\cdot3^2+1\cdot3\cdot4+1\cdot4\cdot3+2\cdot4\cdot5+\ldots+1\cdot9\cdot7 \right )-\newline \hspace*{1.5cm} \ \ -5.6\cdot5.25=\frac{1}{20}\left(635\right )-5.6\cdot5.25=2.35$

Activitat 13

En una classe amb 30 alumnes s'ha estudiat el nombre d'hores diàries d'estudi, X, i el nombre de matèries no superades, obtenint els següents resultats: (2, 1) (0, 7) (1, 2) (3, 0) (3, 1) (1, 1) (1, 2) (2, 0) (3, 1) (3, 0) (2, 7) (1, 0) (2, 1) (1, 1) (3, 1) (1, 4) (1, 2) (2, 1) (3, 1) (1, 4) (1, 2) (2, 1) (2, 0) (3, 1) (2, 2) (1, 0) (1, 2) (2, 1) (0, 6) (2, 0)

Construeix una taula de doble entrada i les taules de freqüències marginals corresponents
Anomenem Y / X=1 a la variable Y condicionada a que X=1 Anomenem X / Y=3 a la variable X condicionada a que Y=3 Construeix les taules condicionades de Y / X=1 i X / Y=3

Diagrama de dispersió o núvol de punts

Aquest és el nom que rep el gràfic que resulta de representar les dades de la variable bidimensional sobre uns eixos de coordenades.

Activitat 14

A partir del següent diagrama de dispersió, construeix la taula de doble entrada i calcula la covariància. Tingues en compte que entre parèntesis s'indica la freqüència de les dades.

Dependència o relació estadística

Es parla de dependència funcional o relació estadística en variables quantitatives quan el núvol de punts de la distribució bivariant tendeix a aproximar-se a la representació gràfica d'una funció. Si el núvol de punts té una forma dispersa i més aviat circular, o sense forma determinada, ens indica que no hi ha dependència, que els valors d'una variable no estàn relacionats, o no influeixen, en els de l'altra variable. En aquest cas es diu que les variables són independents.

La dependència pot ser: a) Exacta, forta o feble. b) Lineal o curvilínea (complexa) c) La dependència lineal pot ser directa (positiva) o indirecta (negativa).

[Extret de l'INS Eugeni d'Ors]

En el següent gràfic tenim dues dependències lineals positives. La primera, forta i l'altra feble.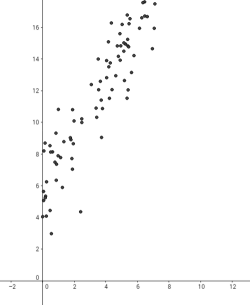

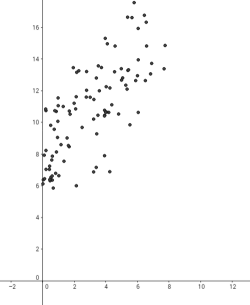
Tanmateix, aquestes serien dues dependències lineals negatives.

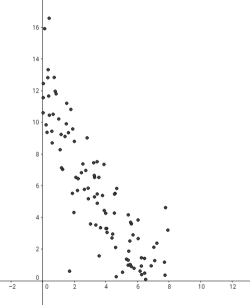
Exemple de dependència lineal

En el següent applet de GeoGebra hem introduït els valors recollits de la variable X i Y. Hem representat el núvol de punts i observem que hi ha una dependència lineal negativa dèbil.

Activitat 15

Modifica els valors de la variable Y de la taula anterior posant els següents: 4 2 3 0 2 4 1 i analitza'n la dependència entre X i Y.

Com es pot estudiar la dependència en variables categòriques o qualitatives? Dues variables qualitatives són independents si cada taula de freqüències condicionada és proporcional a la seva taula de freqüències marginal. Veiem un exemple: Volem estudiar si el gènere (X) influeix a l'hora d'estudiar batxillerat científic-tecnològic o social-humanístic (Y). Tenim la següent taula de doble entrada:

Y \ X	Home	Dona	Total
Científico - Tecnològic	42	63	105
Social - Humanístic	78	117	195
Total	120	180	300

Les taules de freqüències marginals són:

X	n_i	Y	n_i
Home	120	Científico - Tecnològic	105
Dona	180	Social - Humanístic	195
	300		300

Les taules de freqüències condicionades són:

X / Y=Científico - Tecnològic	n_i	X / Y=Social - Humanístic	n_i
Home	42	Home	78
Dona	63	Dona	117
	105		195

Y / X=Home	n_i	Y / X=Dona	n_i
Científico - Tecnològic	42	Científico - Tecnològic	63
Social - Humanístic	78	Social - Humanístic	117
	120		180

Si ens fixem: 42/105 = 78/195 = 120/300 63/105 = 117 /195 = 180/300 42/120 = 63/180 = 105/300 78/120 = 117/180 = 195/300 És a dir, les files i les columnes de la taula de doble entrada, són proporcionals entre elles. Així doncs, les variables gènere i modalitat de batxillerat són independents.

Activitat 16

Tenir gos o gat, X, influeix per aprovar Matemàtiques, Y?

Y \ X	Sí	No
Aprovat	15	20
Suspès	35	50