Drawing Height in Parallelogram and Construct Area Relation
In Figure gived parallelograms ABCD and EFGH and [GI], which is extension of [FG].
Chapter 1: Make the desired operation on the figure according to the following commands.
- Using
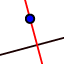icon in Menu draw a segment, which perpendicular to DC, from point A to segment DC in first parallelogram. - With
icon determine the intersection point of this segment and segment DC. - Press "Name" in
button and entitle this point as J. - Draw a straight line, which perpendicular to GI straight line, from point H to GI in second parallelogram by the help of icon.
- Determine a contact point on GI straight line by the help of
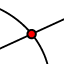icon. - Press the "Name" in
button and entitle this point as K.
- Express the lengths of segments AJ and HK by use of the squares floor.
- How can we correlate segments AJ and HK with a geometric concept
- Express the lengths of segments DC and BC by use of the squares floor.
- Find the area of ABCD parallelogram by use of count of squares. (Tip: Consider that the two half square are a complete square.)
- Find the product lAJl . lDCl and lHKl . lGFl, and compare with area of paralleogram.
- How is the area of the parallelogram calculated?