Voorbeeld + opgaven 23 en 24
Voorbeeld
Je ziet de grafiek van de afgelegde afstand s van een auto op een binnenweg, uitgezet tegen de tijd t. Je ziet dat de snelheid eerst langzaam toeneemt totdat hij na vier minuten maximaal is. De grafiek gaat daar van toenemend stijgend over in afnemend stijgend. Daarna neemt de snelheid weer af. Na acht minuten staat de auto even stil om daarna weer langzaam op te trekken. Bepaal de snelheid van deze auto na precies tien minuten.
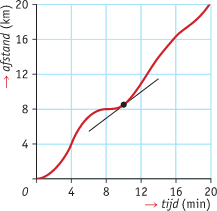
Oplossing:
De snelheid na precies tien minuten is het differentiaalquotiënt op t = 10. Omdat er geen functievoorschrift bij deze grafiek is, bepaal je de waarde van voor t = 10 met behulp van de grafiek en de getekende raaklijn.
Je weet dat de helling is van deze raaklijn.
Je ziet dat die raaklijn behalve door (10;8,5) ook (bij benadering) door het punt (12;10) gaat. De helling van de raaklijn is daarom ongeveer:
De auto had na precies tien minuten een snelheid van 0,75 km/minuut. Dat is ongeveer 45 km/uur.
Opgave 23
In het voorbeeld zie je een tijd afstand-grafiek van een auto.
a. Wanneer was de snelheid van de auto hoger, bij t = 4 of bij t = 16?
b. Wat is de richtingscoëfficiënt van de raaklijn bij t = 8?
c. Hoeveel minuten heeft de auto ongeveer met constante snelheid gereden?
Opgave 24
Je ziet een deel van een grafiek met een punt P op de raaklijn aan de grafiek voor x = 2.
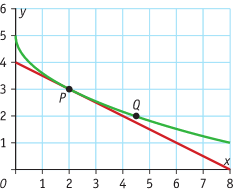
a. Bepaal het differentiaalquotiënt voor x = 2 met behulp van de figuur.
b. Stel een vergelijking van de getekende raaklijn op.
De grafiek hoort bij de functie
Op de grafiek van f ligt ook het punt Q met
c. Stel met de formule voor f en je GR de vergelijking op van de raaklijn in Q.