Pontos Notáveis de um Triângulo
Um dos primeiros polígonos nos qual é apresentado é o triângulo. E, esse fabuloso polígono tem propriedades tão interessantes que foram estudadas e descobertas ao longos do anos pelos matemáticos de todos os lugares.
Poderia citar aqui milhões de propriedade interessantes do triângulo, como por exemplo o Teorema de Pitágoras, as leis trigonométricas, a determinação de um plano e entre outras peculiaridades do nosso amigo triângulo.
Mas, hoje vamos falar de 4 famosos pontos notáveis do Triângulo, que são eles:
O Baricentro, o Incentro, o Circuncentro e o Ortocentro.
Cada um deles tem suas propriedades curiosas e nesse projeto você poderá acompanhar uma possível construção com régua e compasso de cada um deles.
Para encontrar esses 4 pontos, precisamos conhecer 4 retas especiais e são elas:
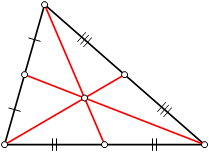
A Mediana de um triângulo é o segmento de reta que liga um vértice deste triângulo ao ponto médio do lado oposto a este vértice. As três medianas se encontram baricentro do triângulo.
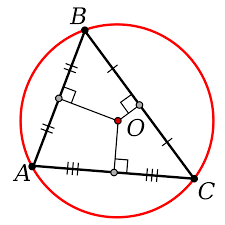
A Mediatriz de um triângulo é uma reta perpendicular a um lado do triângulo que passa pelo seu ponto médio (ponto que equidista dos dois vértices do lado que se toma). As três mediatrizes se encontram no circuncentro triângulo.
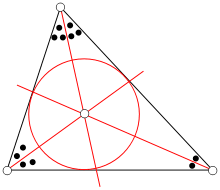
A Bissetriz de um triângulo é a reta que divide um ângulo do triângulo em dois ângulos congruentes. As três bissetrizes se encontram no incentro do triângulo.
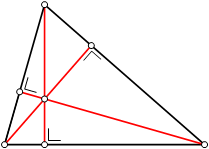
A Altura de um triângulo é a reta perpendicular a um lado do triângulo traçado pelo vértice oposto do triângulo. As três alturas se encontram no ortocentro do triângulo.
Basta provarmos agora, que as três retas de cada tipo se interceptam num único ponto, para fazer isso, vamos ler o seguinte ficheiro:
O Seguinte ficheiro é um capítulo do livro Fundamentos da Matemática Elementar, vol. 9, ed.7. A qual possui as demonstrções, uma lista de exercício e uma breve história sobre Papus de Alexandria.
Um resumo dos Pontos Notáveis:
Espero que tenham gostado do pequeno projeto e até a próxima ;)
